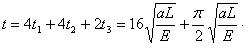问题
计算题
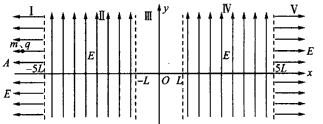
如图所示，在Oxy平面内存在I、Ⅱ、Ⅲ、Ⅳ、Ⅴ五个特殊的电场区域，即在x≤-5L区域I和x≥5L区域Ⅴ存在两个场强大小均为E的匀强电场，方向分别为水平向左和水平向右，在-5L＜x≤-L区域Ⅱ和5L>x≥L区域 Ⅳ存在两个场强大小均为E、方向竖直向上的匀强电场，在
不计粒子的重力）。
（1）粒子到达区域Ⅱ的右边界的速度；
（2）点电荷Q的电荷量；
（3）粒子由静止释放运动到第一次回到初始位置的时间。
答案
解：（1）粒子在电场I中做匀加速直线运动，出区域I时的速度为v0，由动能定理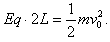
，则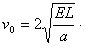
此后在电场Ⅱ中做类平抛运动，则4l=v0t2，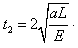
又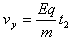
所以粒子到达区域Ⅱ的右边界的速度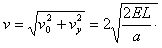
速度与x轴正方向的夹角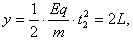
（2）电场Ⅱ中做类平抛运动竖直方向的位移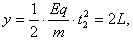
粒子在区域Ⅲ中做匀速圆周运动，则轨道半径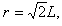
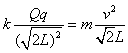，解得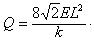
（3）粒子在电场I中做匀加速直线运动的时间
粒子在区域Ⅲ中做匀速圆周运动的时间
粒子穿越区域Ⅳ的时间与穿越区域Ⅱ的时间相同，进人区域V先减速为0，再加速返回，则返回的总时间
