问题
问答题
试证明函数
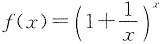 在区间(0,+∞)内单调增加.
在区间(0,+∞)内单调增加.
答案
参考答案:[详解1] 由
 ,有
,有
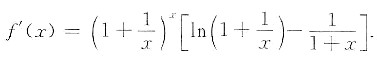
只需证明.对于任意x∈(0,+∞),方括号中的值大于0.
记

对于任意x∈(0,+∞).有
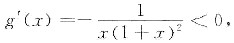
故函数g(x)在(0,+∞)上单调减少.
由于
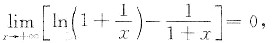
可见,对于任意x∈(0,+∞),有
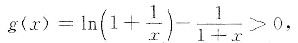
从而f’(x)>0.x∈(0,+∞).
于是,函数f(x)在(0,+∞)上单调增加.
[详解2]
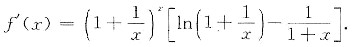
令y=lnx并在区间[x,x+1]对其用拉格朗日中值定理,有

因此,有
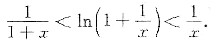
从而,对于任意x∈(0,+∞)有
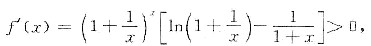
于是,函数f(x)在(0,+∞)上单调增加.
解析:[考点提示] 函数f(x)在(0,+∞)内单调增加的充分条件是f’(x)>0.x∈(0,+∞).因此只需证明:对任意x∈(0,+∞)有f’(x)>0.
