问题
问答题
假设X1，X2，…，Xn为来自总体X的简单随机样本，已知E(Xk)=ak(k=1，2，3，4)．证明：当n充分大时，随机变量
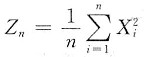近似服从正态分布，并指出其分布参数．
答案
参考答案：依题意X1，X2，…，Xn独立同分布，可知
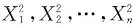也独立同分布，由E(Xk)=ak(k=1，2，3，4)有
，
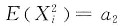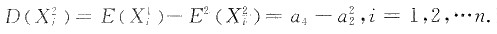
于是
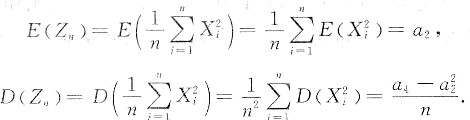
因此根据独立同分布的(列维-林德伯格)中心极限定理，当n充分大时，
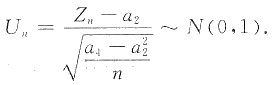
故当n充分大时，
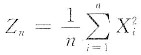近似服从参数为
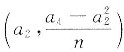的正态分布．
解析：[评注] 本题主要考查独立同分布的(列维-林德伯格)中心极限定理的条件和结论，及简单随机样本的概念与数学期望、方差的性质．
[考点提示] 利用独立同分布的(列维-林德伯格)中心极限定理即可，关键在于计算Zn的数学期望和方差．