问题
解答题
(本小题共13分)
某同学设计一个摸奖游戏:箱内有红球3个,白球4个,黑球5个.每次任取一个,有放回地抽取3次为一次摸奖.至少有两个红球为一等奖,记2分;红、白、黑球各一个为二等奖,记1分;否则没有奖,记0分.
(I)求一次摸奖中一等奖的概率;
(II)求一次摸奖得分的分布列和期望.
答案
解:(I)每次有放回地抽取,取到红球的概率为 ;取到白球的概率为
;取到白球的概率为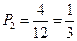 ;取到
;取到
黑球的概率为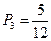 ;-------------3分
;-------------3分
一次摸奖中一等奖的概率为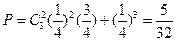 . ---------5分
. ---------5分
(II)设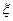 表示一次摸奖的得分,则
表示一次摸奖的得分,则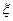 可能的取值为0,1,2. -----------6分
可能的取值为0,1,2. -----------6分
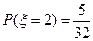 ;
;
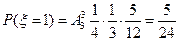 ;---------8分
;---------8分
 ---10分
---10分
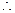 一次摸奖得分
一次摸奖得分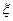 的分布列为
的分布列为
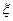 | 2 | 1 | 0 |
| P | 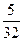 |  |  |
 . -------------------13分
. -------------------13分 