设a和b分别是先后抛掷一枚骰子得到的点数，且随机变量ξ表示方程

问题解答题

设a和b分别是先后抛掷一枚骰子得到的点数，且随机变量ξ表示方程ax²+bx+1=0的实根的个数（相等的两根算一个根）．

（1）求方程ax²+bx+1=0无实根的概率；

（2）求随机变量ξ的概率分布列；

（3）求在先后两次出现的点数中有4的条件下，方程ax²+bx+1=0有实根的概率．

答案

基本事件总数为：6×6=36

（1）若方程无实根，则△=b²-4a＜0即b²＜4a

若a=1，则b=1，

若a=2，则b=1，2

若a=3，则b=1，2，3

若a=4，则b=1，2，3

若a=5，则b=1，2，3，4

若a=6，则b=1，2，3，4

∴目标事件个数为1+2+3+3+4+4=17

因此方程ax2+bx+1=0有实根的概率为

…（6分）

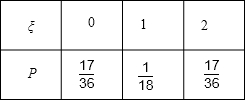
（2）由题意知，ξ=0，1，2，

则P(ξ=0)=

，P(ξ=1)=

，P(ξ=2)=

，

故ξ的分布列为

（3）记“先后两次出现的点数中有4”为事件M，

“方程ax²+bx+1=0有实根”为事件N，则

P(M)=

，P(MN)=

，P(N/M)=

P(MN)

P(M)

…（4分）