甲、乙两人同时参加奥运志愿者选拔赛的考试,已知在备选的10道题中,甲能答对其中的6道题,乙能答对其中的8道题.规定每次考试都从备选题中随机抽出3道题进行测试,至少答对2道题才能入选.
(I)求甲答对试题数ξ的分布列及数学期望;
(II)求甲、乙两人至少有一人入选的概率.
(I)依题意,甲答对试题数ξ的可能取值为0,1,2,3,
则P(ξ=0)=
=C 34 C 310
,1 30
P(ξ=1)=
=
•C 16 C 24 C 310
,3 10
P(ξ=2)=
=
•C 26 C 14 C 310
,1 2
P(ξ=3)=
=C 36 C 310
..1 6
∴ξ的分布列为
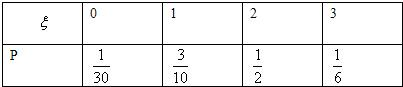
甲答对试题数ξ的数学期望为Eξ=0×
+1×1 30
+2×3 10
+3×1 2
=1 6
.9 5
(II)设甲、乙两人考试合格的事件分别为A、B,则P(A)=P(ξ=2)+P(ξ=3)=
,P(B)=2 3
=C 28
+C 12 C 38 C 310
=56+56 120
.14 15
因为事件A、B相互独立,
∴甲、乙两人考试均不合格的概率为P(
•. A
)=P(. B
)•P(. A
)=[1-. B
][1-2 3
]=14 15
.1 45
∴甲、乙两人至少有一人考试合格的概率为P=1-P(
•. A
)=1-. B
=1 45
.44 45
故甲、乙两人于少有一人考试合格的概率为
..44 45
