问题
解答题
（本小题12分）袋中有形状大小完全相同的8个小球，其中红球5个，白球3个。某人逐个从袋中取球，第一次取出一个小球，记下颜色后放回袋中；第二次取出一个小球，记下颜色后，不放回袋中，第三次取出一个小球，记下颜色后，放回袋中，第四次取出一个小球，记下颜色后不放回袋中……，如此进行下去，直到摸完球为止。
（1）求第四次恰好摸到红球的概率；
（2）记ξ为前三次摸到红球的个数，写出其分布列，并求其期望Eξ。
答案
（1）5/14，（2）同解析
解：（1）第一和第三次取球对第四次无影响，计第四次摸红球为事件A
①第二次摸红球，则第四次摸球时袋中有4红球概率为
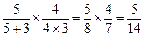（2分）
②第二次摸白球，则第四次摸球时袋中有5红2白，摸红球概率为
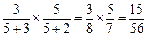（3分）
∴P(A)=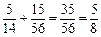
，即第四次恰好摸到红球的概率为
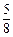。（6分）
（2）由题设可知ξ的所有可能取值为：ξ=0，1，2，3。P（ξ=0）=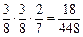
；
P（ξ=1）=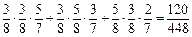
；P（ξ=2）=
；
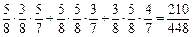P（ξ=3）=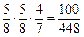
。故随机变量ξ的分布列为：
| ξ | 0 | 1 | 2 |
| |
| P |  |  |  |  |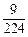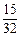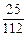
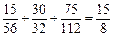（个），故Eξ=
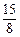（个） （1