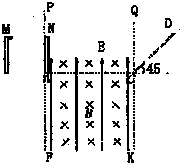
如图所示,两块平行金属板M、N竖直放置,板长为L,两板间距为d,且L=d=0.4m,两板间的电势差U=1.0×103V,竖直边界PF、QK之间存在着正交的匀强电场和匀强磁场,其中电场强度E=2.5×103N/C,方向竖直向上;磁感应强度B=1.0×103T,方向垂直纸面向里;C点与N板下端点A在同一水平线上.光滑绝缘斜面CD足够长,倾角为45°,斜面底端与C点重合,现将一电荷量q=+4.0×10-5C的带电小球自M板上边缘由静止释放,沿直线运动到A点后进入叠加场区域,恰好从C点滑上斜面CD.若重力加速度g=10m/s2,求:
(1)带电小球的质量.
(2)A点到C点的距离.
(3)带电小球沿斜面CD上滑的最大高度.
(1)由L=d可知,MA与水平方向成45°角,所以,带电小球在两金属板间沿直线MA运动时,有mg=q
,m=U d
=1×10-2kg ①qU gd
(2)小球在由M点运动到A点的过程中,
由动能定理得 mgL+qU=
mv2,1 2
解得v=
=4m/s.②4gL
小球在正交的匀强电场和匀强磁场中,由于mg=qE=0.1N,所以由A到C做匀速圆周运动,

由牛顿第二定律得 qvB=mv2 R
解得:轨道半径R=
=1m ③mv qB
由几何关系得∠AOC=90°,所以A、C两点间的距离SAC=
R=2
m,④2
(3)小球达到C点的速度大小v=4m/s,方向与水平方向成45°角,⑤
小球沿斜面上滑过程中,由机械能守恒
mv2=mgH,1 2
解得小球沿斜面CD上滑的最大高度H=0.8m⑥
答:
(1)带电小球的质量为1×10-2kg.
(2)A点到C点的距离是
m.2
(3)带电小球沿斜面CD上滑的最大高度是0.8m.
