质量m=1.0kg的甲物体与竖直放置的轻弹簧的上端连接,弹簧下端固定在地面上,如右图所示.质量m=1.0kg的乙物体从甲物体正上方,距离甲物体h=0.40m处自由落下,撞在甲物体上在极短的时间内与甲物体粘在一起(不再分离)向下运动.它们到达最低点后又向上运动,上升的最高点比甲物体初始位置高H=0.10m.已知弹簧的劲度系数k=200N/m,且弹簧始终在弹性限度内,空气阻力可忽略不计,重力加速度g取10m/s2.求:
(1)乙物体和甲物体碰撞过程中损失的动能;
(2)乙物体和甲物体碰撞后一起向下运动的最大距离.
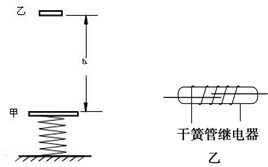
(1)设乙物体和甲物体碰撞前瞬间乙物体的速度大小为v1,
根据v12=2gh 解得v1=2
m/s=2.8 m/s2
设乙物体和甲物体碰撞后的共同速度大小为v2,
由动量守恒定律有mv1=2mv2
解得v2=
v1=1 2
m/s=1.4 m/s2
则碰撞后系统的动能Ek2=
(2m)v22=2 J 1 2
甲、乙物体构成的系统碰撞前的动能Ek1=4 J,故乙物体和甲物体碰撞过程中损失的机械能
△E=Ek1-Ek2=2 J
(2)设甲物体静止时弹簧压缩量为x1,根据平衡条件,
解得x1=
=5.0 cmmg k
甲和乙碰撞后做简谐运动,在通过平衡位置时两物体所受合力为零,速度最大,设此时弹簧压缩量为x2,
解得x2=
=10 cm2mg k
甲物体和乙物体一同上升到最高点,两物体与简谐运动平衡位置的距离,即简谐运动的振幅
A=x2+(H-x1)=15 cm
根据简谐运动的对称性可知,两物体向下运动的最大距离
x=A+(x2-x1)=20 cm
答:(1)乙物体和甲物体碰撞过程中损失的动能为2J;
(2)乙物体和甲物体碰撞后一起向下运动的最大距离0 20cm.
