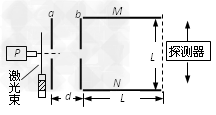
飞行时间质谱仪可以根据带电粒子的飞行时间对气体分子进行分析。如图所示，在真空状态下，自脉冲阀P喷出微量气体，经激光照射产生不同正离子，自a板小孔进入a、b间的加速电场，从b板小孔射出，沿中线方向进入M、N板间的方形区域，然后到达紧靠在其右侧的探测器。已知极板a、b间的电压为U0，间距为d，极板M、N的长度和间距均为L。不计离子重力及经过a板时的初速度。
（1）若M、N板间无电场和磁场，请推导出离子从a板到探测器的飞行时间t与比荷k（k=
，q和m分别为离子的电荷量和质量）的关系式；
（2）若在M、N间只加上偏转电压U1，请论证说明不同正离子的轨迹是否重合；
（3）若在M、N间只加上垂直于纸面的匀强磁场。已知进入a、b间的正离子有一价和二价的两种，质量均为m，元电荷为e。要使所有正离子均能通过方形区域从右侧飞出，求所加磁场的磁感应强度的最大值Bm。
解：（1）带电离子在平行板a、b间运动时，根据动能定理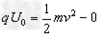 
①
解得：
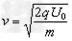，即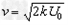
带电离子在平行板a、b间的加速度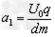
，即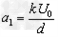
所以，带电离子在平行板a、b间的运动时间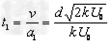
带电离子在平行板M、N间的运动时间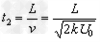
所以，带电离子的全部飞行时间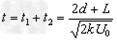
（2）正离子在平行板M、N间水平方向运动位移为x时，在竖直方向运动的位移为y
水平方向满足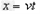
②
竖直方向满足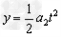
③
加速度
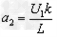④
由上述②、③、④式得：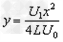
⑤
⑤式是正离子的轨迹方程，与正离子的质量和电荷量均无关。所以，不同正离子的轨迹是重合的
（3）当M、N间磁感应强度大小为B时，离子做圆周运动，满足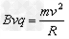
⑥
由上述①、⑥两式，解得：带电离子的轨道半径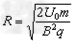
⑦
上式表明：在离子质量一定的情况下，离子的电荷量越大，在磁场中做圆周运动的半径越小，也就越不容易穿过方形区从右侧飞出。所以，要使所有的一价和二价正离子均能通过方形区从右侧飞出，只要二价正离子能从方形区飞出即可。当二价正离子刚好能从方形区域飞出时的磁感应强度为满足题目条件的磁感应强度的最大值
设当离子刚好通过方形区从右侧飞出时的轨道半径为R，由几何关系得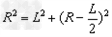
解得：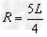
⑧
将二价正离子的电量2e代入⑦式得：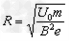
⑨
由⑧、⑨式得：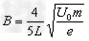
，此值即为所求的磁感应强度的最大值Bm