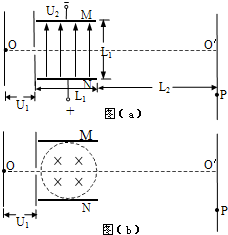
如图(a)所示,电子从加速电场的O点发出(初速不计),经电压为U1的加速电场加速后沿中心线进入两平行金属板M、N间的匀强电场中,通过电场后打到荧光屏上的P点处,设M、N板间的电压为U2,两极板间距离与板长相等,均为L1,板的右端到荧光屏的距离为L2,已知U1=200V,U2=300V,L1=6cm,L2=21cm,电子的比荷e/m=1.8×1011C/kg.求:
(1)电子离开偏转电场时的偏角θ的正切函数值tanθ(若可以求出具体角度也行);
(2)电子打到荧光屏上的位置P偏离荧光屏中心O′的距离Y;
(3)若撤去M、N间的电压U2,而在两平行板间直径为L1的圆形区域内加一方向垂直纸面向里的匀强磁场(如图b所示,圆心恰好在平行板的正中间),要使电子通过磁场后仍打在荧光屏上的P点处,则电子在磁场中的轨道半径为多大?磁感应强度B的大小为多大?
(1)对加速阶段应用动能定理,有:
eU1=m
解得:v0=
偏转阶段类平抛轨迹如图a所示,可以得到:
tanθ======
所以θ=37°
(2)经过偏转电场时的偏转距离y=()2==cm=2.25cm
从偏转电场出来后作直线运动:由=
得Y=y=×2.25cm=18cm
[或直接求Y=(L2+)tanθ=(21+3)×cm=18cm]
(3)如图乙所示,电子轨迹从磁场出来的切线延长线交于磁场区的圆心,因为也打在P点,所以θ=37°
由图可知电子轨道半径R满足:
Rsinθ=+cosθ
解之得:
R==cm=9cm
又R=
得B====×10-4=5.24×10-4T
答:(1)电子离开偏转电场时的偏角θ的正切函数值tanθ为;
(2)电子打到荧光屏上的位置P偏离荧光屏中心O′的距离Y为18cm;
(3)电子在磁场中的轨道半径为9cm,磁感应强度B的大小为5.24×10-4T.