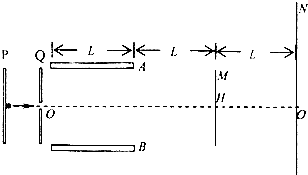
如图所示,加速电场PQ间的加速电压为U1,一不计重力的带正电粒子由静止开始经加速电场加速后,沿偏转电场AB(内部看成是匀强电场,忽略外部周围产生的电场)的中心线OO'以垂直电场的方向进入偏转电场.已知偏转电场的电压恒为U2=20V,A极板带正电,极板长L=24cm,极板间距d=24cm.有一长度也为d的固定挡板M放在距AB的右端为L处,与OO'垂直,中点H在OO'上,在挡板M的右侧L处有一足够大的荧光屏N垂直OO'放置.调整加速电压U1可以使粒子打到荧光屏上.
(1)求粒子打到光屏上的位置距O'最远时,粒子离开偏转电场时的速度方向与进入时速度方向的夹角及最远位置距O'点的距离.
(2)求粒子能够打到荧光屏上的范围及所对应的加速电压U1满足的条件.
(1)粒子在加速电场中有:q=
在偏转电场中偏转距离为y,速度偏角为φ:
L=t,a=,y=,tanφ=
可求出在偏转电场中的偏转距离为:
y=,tanφ=
由此可知越小y、tanφ越大,打到屏幕上的位置越远,当y=时最远,此时满足=,解得=10V,即=10V时粒子离O′最远,且tanφ=1,所以φ=45°.
由图可得打到屏幕上的距离Y=y+2Ltanφ,代入数据可得Y=60cm.
故最远时,粒子离开偏转电场时的速度方向与进入时速度方向的夹角及最远位置距O'点的距离为60cm.
(2)由上问越大y、tanφ越大,打到屏幕上的位置越远,当从偏转电场出射的粒子恰好能经过固定挡板M时,打到屏上的位置离最近,则有:
=y+Ltanφ,=,=+
可得==30V,tanφ=
打到光屏上的位置距的距离为:=y+2Ltanφ=20cm
可见粒子能够打到荧光屏上的范围是距离从20cm到60cm处,对应加速电压是从30V到10V.
故粒子能够打到荧光屏上的范围是从20cm到60cm,所对应的加速电压满足的条件为30V到10V.