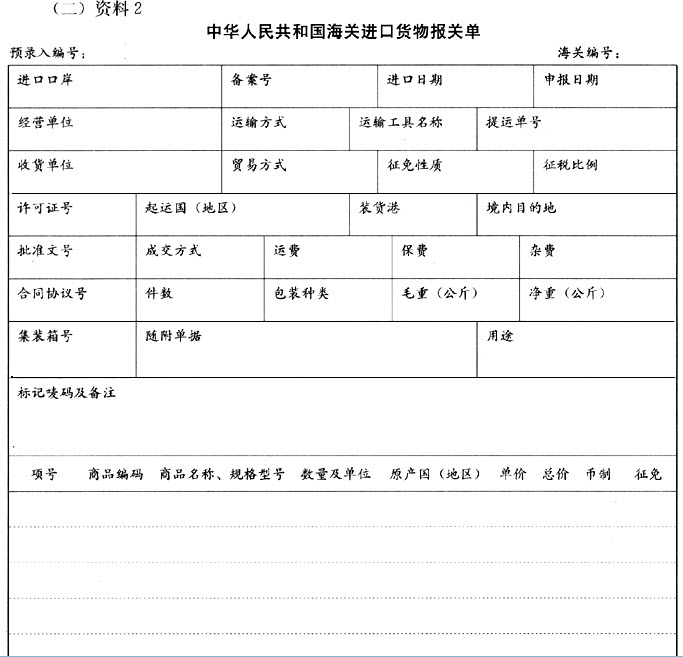
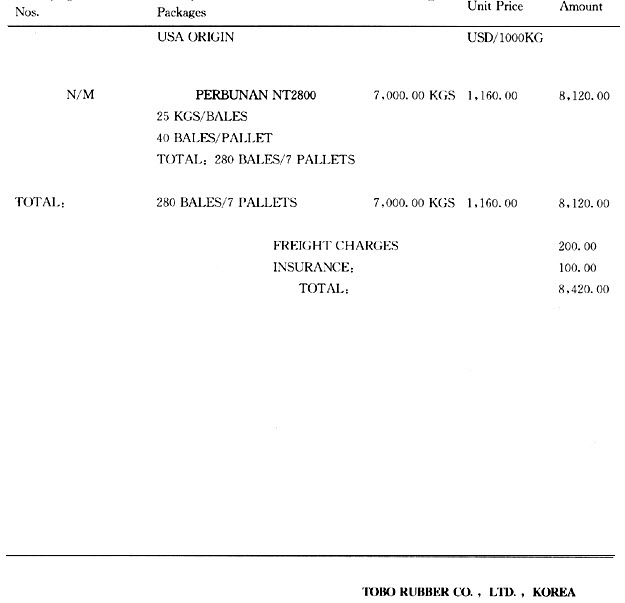
问题
解答题
一个袋子装有大小形状完全相同的9个球,其中5个红球编号分别为1,2,3,4,5,4个白球编号分别为1,2,3,4,从袋中任意取出3个球.
(1)求取出的3个球编号都不相同的概率;
(2)记X为取出的3个球中编号的最小值,求X的分布列与数学期望.
答案
(1)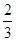 (2)
(2)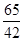
记“取出的3个球编号都不相同”为事件A,“取出的3个球中恰有两个球编号相同”为事件B,则P(B)=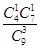 =
=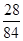 =
=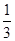 ,∴P(A)=1-P(B)=
,∴P(A)=1-P(B)=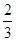 .
.
(2)X的取值为1,2,3,4
P(X=1)=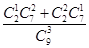 =
=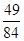 ,P(X=2)=
,P(X=2)= =
=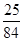 ,
,
P(X=3)= =
=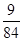 ,P(X=4)=
,P(X=4)=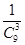 =
=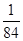 .
.
所以X的分布列为
| X | 1 | 2 | 3 | 4 |
| P | 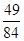 | 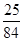 | 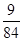 | 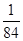 |
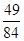 +2×
+2×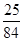 +3×
+3×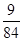 +4×
+4×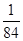 =
=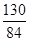 =
=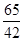 .
.