问题
问答题
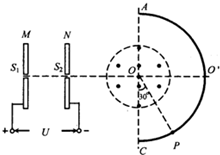
如图所示,M、N是竖直正对放置的两个平行金属板,S1、S2是M、N板上的两个小孔;N板的右侧有一个在竖直面内,以O为圆心的圆形区域,该区域内存在垂直圆面向外的匀强磁场,另有一个同样以O为圆心的半圆形荧光屏AO’C;已知S1、S2、O和荧光屏的中间位置O’在同一直线上,且AC⊥S1O’.当在M、N板间加恒定电压U时,一带正电离子在S1处由静止开始加速向S2孔运动,最后打在图示的荧光屏上的P处,∠COP=30°.若要让上述带电离子(不计重力)仍在S1处静止开始加速,最后打在图示的荧光屏下边缘C处,求M、N板间所加电压的大小.
答案
设离子的质量为m、电荷量为q,磁场的磁感应强度为B、所在区域的半径为R,离子加速后获得的速度为v
当电压为U时,由动能定理有 qU=
mv2 ①1 2
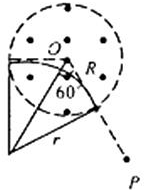
在磁场中,离子做匀速圆周运动(见右图)
由牛顿第二定律可知 qvB=m
②v2 r
由①②式得 U=
③r2B2q 2m
其中,r=Rtan60°=
R ④3
当电压为U′时,离子打在C处
同理有U′=
⑤r′2B2q 2m
其中,r′=R ⑥
由③④⑤⑥可解得U′=
U1 3
答:M、N板间所加电压的大小为
U.1 3
