如图甲所示,建立Oxy坐标系,两平行极板P、Q垂直于y轴且关于x轴对称,极板长度和板间距均为l,第一四象限有磁场,方向垂直于Oxy平面向里.位于极板左侧的粒子源沿x轴间右连接发射质量为m、电量为+q、速度相同、重力不计的带电粒子在0~3t0时间内两板间加上如图乙所示的电压(不考虑极边缘的影响).
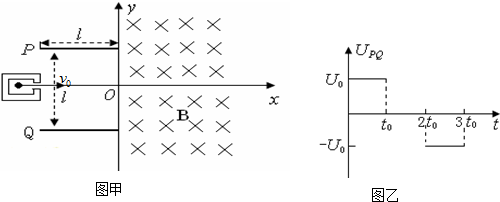
已知t=0时刻进入两板间的带电粒子恰好在t0时,刻经极板边缘射入磁场.上述m、q、l、t0、B为已知量.(不考虑粒子间相互影响及返回板间的情况)
(1)求电压U0的大小.
(2)求t0时刻进入两板间的带电粒子在磁场中做圆周运动的半径.
(3)带电粒子在磁场中的运动时间.
(1)t=0时刻进入两极板的带电粒子在电场中做匀变速曲线运动,t0时刻刚好从极板边缘射出,在y轴负方向偏移的距离为
,则有 E=l 2 U0 l
Eq=ma
=l 2
at021 2
联立解得,两极板间偏转电压为U0=
.ml2 qt02
(2)t0时刻进入两极板的带电粒子,两极板没有电场,带电粒子做匀速直线运动.
带电粒子沿x轴方向的分速度大小为v0=l t0
设带电粒子离开电场进入磁场做匀速圆周运动的半径为R,则有qvB=mv02 R
联立解得,R=ml qBt0
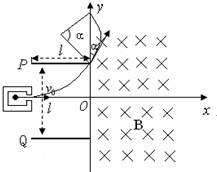
(3)2t0时刻进入两极板的带电粒子在磁场中运动时间最短.带电粒子离开电场时沿y轴正方向的分速度为vy=at0,
设带电粒子离开电场时速度方向与y轴正方向的夹角为α,则
tanα=v0 vy
联立解得α=
,带电粒子在磁场运动的轨迹图如图所示,圆弧所对的圆心角为2α=π 4
,所求最短时间为 tmin=π 2
T.1 4
带电粒子在磁场中运动的周期为T=
,联立以上两式解得2πm qB
tmin=
.πm 2qB
同理,t=0进入两极板的带电粒子在磁场中运动的时间最长为:tmax=3πm 2qB
所以,带电粒子在磁场中的运动时间:
≤t≤πm 2qB
.3πm 2qB
答:
(1)电压U0的大小为U0=
.ml2 qt02
(2)t0时刻进入两板间的带电粒子在磁场中做圆周运动的半径R=
.ml qBt0
(3)带电粒子在磁场中的运动时间为
≤t≤πm 2qB
.3πm 2qB
