问题
问答题
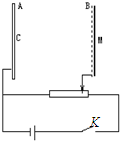
如图所示,在铅板A中心处有个放射源C,它能向各个方向不断地射出速度大小相等的电子流,B为金属网,M为紧靠B外侧的荧光屏.A和B接在电路中,它们相互平行且正对面积足够大.已知电源电动势为ε,滑动变阻器的最大电阻是电源内阻r的4倍,A、B间距为d,电子质量为m,电量为e,不计电子形成的电流对电路的影响,忽略重力的作用.
(1)当滑动变阻器的滑片置于中点时,求闭合电键K后,AB间的场强E的大小.
(2)若移动滑动变阻器的滑片,荧光屏上得到最小的亮斑面积为S,试求电子离开放射源时的速度大小.
答案
(1)设电源内阻为r,则变阻器的总阻值为4r.
当滑动变阻器的滑片位于中点时,
根据闭合电路欧姆定律得:I=
=ε r+4r ε 5r
AB间的电势差为:UAB=I2r=
?2r=ε 5r 2ε 5
所以电场强度为:E=
=UAB d
.2ε 5d
(2)荧光屏上的亮斑面积大小由初速度沿竖直方向的粒子在该方向上的位移R决定,即:S=πR2
粒子在做类平抛运动,
所以:R=v0t,
d=1 2
t2,eUAB dm
当变阻器的阻值取4r时,UAB最大,此时电子在AB间运动的时间最短:Um=
,4ε 5
由上述方程解得:v0=1 d
.2eεS 5πm
