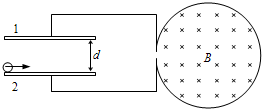
如图所示,一半径为r的圆形导线框内有一匀强磁场,磁场方向垂直于导线框所在平面,导线框的左端通过导线接一对水平放置的平行金属板,两板间的距离为d,板长为l,t=0时,磁场的磁感应强度B从B0开始均匀增大,同时,在板2的左端且非常靠近板2的位置有一质量为m、带电量为-q的液滴以初速度v0水平向右射入两板间,该液滴可视为质点.
(1)要使该液滴能从两板间射出,磁感应强度随时间的变化率K应满足什么条件?
(2)要使该液滴能从两板间右端的中点射出,磁感应强度B与时间t应满足什么关系?
解 (1)由题意可知:板1为正极,板2为负极
设磁场变化率为K,两板间的电压:U=
=s△∅ △t
=sK ①△B △t
而:s=πr2 ②
带电液滴受的电场力:F=Eq=
q ③U d
由牛顿第二定律得:F-mg=ma ④
由③④联立解得:a=
-g ⑤uq dm
由于极板1带正电,液滴受到向上电场力,若重力大于电场力,小球将沿极板直线飞出;
若重力小于电场力,液滴将向上偏转,做类平抛运动,当刚好沿上极板飞出时有:
x=l=vt ⑥
y=d=
at2= 1 2
(1 2
-g)Uq dm
⑦l2 v2
由②⑦得:K=2md2
+gdml2v 20 πqr2l2
要使液滴能射出,必须满足 y<d
故磁感应强度随时间的变化率满足条件为:K<K1
(2)当液滴从两板右端中点射出时,有:
l=v0t,⑧
=d 2
at2 ⑨1 2
联立①⑤⑧⑨解得此时磁感应强度的变化率为:K=md2
+gdml2v 20 πqr2l2
所以磁感应强度B与时间t应满足关系为:B=B0+
tmd2
+gdml2v 20 πqr2l2
