问题
问答题
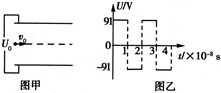
一电子(质量m=0.91×10-30kg,电荷量q=1.6×10-19C)从静止开始经电压为U0=182V的加速电场加速后,t=0时刻从两平行金属极板的中线处平行于极板射入,如图甲所示.两极板相距d=0.1m,两极板之间加上如图乙所示的交变电压,最后电子刚好从某一极板边缘飞出.不计电子所受重力,求:
(1)电子离开极板时的动能为多少eV;
(2)极板的长度L.
答案
(1)电子经过加速电场的加速,则有:qU0=
m1 2 v 20
解得:v0=8.0×106m/s
电子在偏转电场中1.0×10-8s内,在垂直极板的方向做匀加速直线运动,设电子的加速度为a,垂直极板方向的位移为y,则:
a=
=F m
,y=qU md
at21 2
解得:y=8.0×10-3m<
d1 2
所以电阻在偏转磁场中在垂直极板的方向先做匀加速再做匀减速,再加速,再减速…
设电子经过n个加速、减速的过程,则:2n•y≤
d1 2
解得:n≤3.125,所以取n=3
即经过加速、减速各3次后电阻距离极板的距离:△y=
d-2y×3=2×10-3m且经过这几次的加速、减速后电子的动能不会变,1 2
电子在剩余的距离上加速对应的电势差:△u=U
=1.82V△y d
所以电子离开电场时的动能:EK=q(U0+△u)=183.82eV
(2)电子偏转△y=2.0×10-3m使用的时间:t1:
△y=
a1 2
,解得:t1=0.5×10-8st 21
电子在极板中运动的总时间:t=3T+t1=6.5×10-8s
所以极板的长度:L=v0t=0.52m
答:(1)电子离开极板时的动能为183.82eV;
(2)极板的长度是0.52m.
