问题
解答题
若二项式(1+2x)n展开式中第6项与第7项的系数相等,求展开式中二项式系数最大的项和系数最大的项.
答案
解:∵在(1+2x)n的展开式中第六项与第七项的系数相等,
∴Cn525=Cn626,
∴n=8,
∴展开式中二项式系数最大的项是第5项: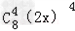 =1120x4.
=1120x4.
二项式的展开式的系数系数最大的项为第r项,
所以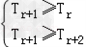 ,即
,即 ,
,
解得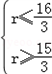 ,
,
所以r=5,
所以展开式中系数最大的项是第5项.
若二项式(1+2x)n展开式中第6项与第7项的系数相等,求展开式中二项式系数最大的项和系数最大的项.
解:∵在(1+2x)n的展开式中第六项与第七项的系数相等,
∴Cn525=Cn626,
∴n=8,
∴展开式中二项式系数最大的项是第5项: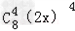 =1120x4.
=1120x4.
二项式的展开式的系数系数最大的项为第r项,
所以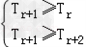 ,即
,即 ,
,
解得 ,
,
所以r=5,
所以展开式中系数最大的项是第5项.