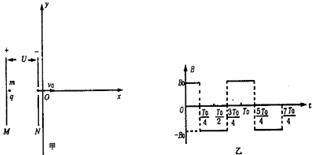
如图甲所示,在y轴右侧(包括y轴)存在如图乙所示变化的均匀磁场,其变化周期为T0,规定垂直xOy平面向里的磁场方向为正.在y轴左侧有竖直放置的平行金属板M、N,两板间的电势差为U,一质量为m、电荷量为q的带正电粒子,从M板的中点无初速释放,通过N板小孔后从坐标原点沿x轴正方向射入磁场(粒子重力和空气阻力均不计).
(1)求粒子在磁场中运动的轨道半径r.
(2)若T0=,粒子在t=0时刻从O点射入磁场中,求t=T0时粒子的位置坐标.
(3)若T0=,粒子在t=时刻从O点射入磁场中,求t=T0时粒子的坐标.
(1)设粒子被电场加速获得速度大小为v0,
据动能定理有qU=m
解得v0=
粒子垂直进入磁场后做半径为r的匀速圆周运动,
则qv0B0=m
得r==
(2)设粒子在磁场中运动的周期为T,
则T===T0
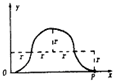
所以,当t=0时刻从O点射入磁场中,在T0时间内,粒子先用了时间做逆时针方向的匀速圆周运动,
接着用时间做顺时针方向的匀速圆周运动,最后用了时间做逆时针方向的匀速圆周运动到达x轴上的P点,如图所示,
则OP=4r=4
P点的位置坐标为(4,0)
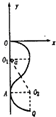
(3)由于T0==t,从到T0的内,
则有=T=T
即磁场变化半个周期内粒子运动转过150°角,经T0时间粒子到达Q点轨迹如图,由几何关系α=60°,=sinα
Q点的横坐标xQ=r=
纵坐标v0=++=(2+)r=(2+)
即Q点的位置坐标为(,(2+))
答:(1)求粒子在磁场中运动的轨道半径r=.
(2)若T0=,粒子在t=0时刻从O点射入磁场中,则t=T0时粒子的位置坐标为(4,0).
(3)若T0=,粒子在t=时刻从O点射入磁场中,则t=T0时粒子的坐标为
(,(2+)).