问题
问答题
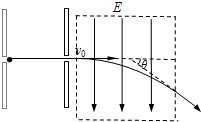
如图所示,质量为m,电荷量+q的带电粒子在左侧加速电场的作用下,以速度v0进入场强为E的偏转电场,在偏转电场的作用下偏转θ角射出.若撤去电场改用同样宽度的匀强磁场,使该离子通过该区域并使偏转角度也为θ,求
(1)加速电场的电压;
(2)所加磁场的磁感应强度为多大;
(3)粒子穿过电场和磁场的时间之比为多少.
答案
(1)由动能定理得,qU=
mv021 2
解得:U=
.mv02 2q
(2)设电场的宽度为L,粒子在偏转电场中做类平抛运动
运动时间t=L v0
粒子在偏转电场中的加速度a=qE m
tanθ=
=at v0
①qEL mv02
粒子在磁场中做匀速圆周运动向心力,由洛伦兹力提供:qv0B=mv02 R
解得R=mv0 qB
由几何关系得:sinθ=
=L R
②qBL mv0
由①②联立解得B=
.Ecosθ v0
(3)粒子在偏转电场中运动的时间t电=
③L v0
粒子在磁场中运动的时间t磁=
④θ?m qB
由②③④联立解得
=t电 t磁 sinθ θ
答:(1)加速电场的电压为
.mv02 2q
(2)所加磁场的磁感应强度为
.Ecosθ v0
(3)粒子穿过电场和磁场的时间之比为
=t电 t磁
.sinθ θ
