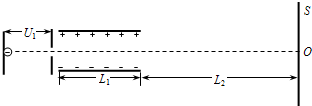
下面是一个示波管工作原理图,初速度为零的电子经电压为U1的电场加速后垂直进入偏转电场,两平行板间的距离为d,板长L1,偏转电压为U2.S为屏,与极板垂直,到极板的距离L2.已知电子电量e,电子质量m.不计电子所受的重力.
(1)电子进入偏转电场的速度v0是多少?
(2)电子离开偏转电场时的偏转量y1为多少?(用U1、U2、d、L1表示)
(3)电子到达屏S上时,它离O点的距离y是多少?(用U1、U2、d、L1、L2表示)
(1)设电子经加速电场U1加速后以速度v0进入偏转电场,由动能定理有
qU1=
mv02,v0=1 2 2qU1 m
故电子进入偏转电场的速度 v0=2qU1 m
(2)进入偏转电场后在电场线方向有,a=qU2 md
经时间t1飞出电场有t1=
,飞出电场时偏转量为 y1=L1 v0
at12 1 2
由以上各式得 y1=U2L12 4dU1
故电子离开偏转电场时的偏转量y1=U2L12 4dU1
(3)设电子从偏转场穿出时,沿y方向的速度为vy,穿出后到达屏S所经历的时间为t2,在此时间内电子在y方向移动的距离为y2,有
vy=at1 t2=
y2=vyt2 L2 v0
由以上各式得
y2=U2L2L1 2dU1
y=y1+y2=
(L1+2L2)U2L1 4dU1
也可用相似比直接求y.即:
=y y1
,y=
+L2L1 2 L1 2
y1=(L1+2L2)L1+2L2 L1 U2L1 4dU1
故电子到达屏S上时,它离O点的距离y=y1+y2=
(L1+2L2).U2L1 4dU1