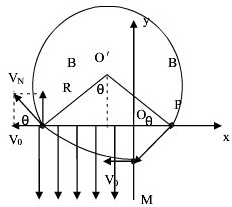
如图所示,在直角坐标系的第一、二象限内有垂直于纸面的匀强磁场,第三象限有沿Y轴负方向的匀强电场,第四象限内无电场和磁场.质量为m、带电量为q的粒子从M点以速度v0沿x轴负方向进入电场,不计粒子的重力,粒子经N、P最后又回到M点.设OM=L,ON=2L,则:
(1)电场强度E的大小;
(2)匀强磁场的磁感应强度B的大小和方向;
(3)粒子从M点进入电场,经NP点最后又回到M点所用的总时间.

(1)由带电粒子在电场中做类平抛运动,易知L=1 2
t2,且2L=v0t则:qE m
E=mv02 2qL
(2)由左手定则,匀强磁场的方向为垂直纸面向里.
根据粒子在电场中运动的情况可知,粒子带负电.粒子在电场中做类平抛运动,设到达N点的速度为v,运动方向与x轴负方向的夹角为θ,如图所示.
由动能定理得:qEL=
mv 2-1 2
mv021 2
将(1)中的E代入可得:v=
v0 所以θ=45°2
粒子在磁场中做匀速圆周运动,经过P点时速度方向也与x轴负方向成45°角.
则OP=OM=L
NP=NO+OP=3L
粒子在磁场中的轨道半径为R=NPcos45°=
L 又 R=3 2
解得B=mv Bq
,方向垂直纸面向里.2mv0 3qL
(3)分类平抛运动时间和在磁场中的运动时间,PM的匀速直线运动时间.
粒子在电场中运动的时间为 t1=2L v0
设粒子在磁场中运动所用的时间为t2,有
t2=
T=3 4
×3 4
=2πm Bq 9πL 4v0
从P离开磁场作匀速直线运动到M所用的时间为t3,
t3=
=
L2 v L v0
粒子从M点进入电场,经N、P点最后又回到M点所用的时间为:
t=t1+t2+t3=(3+
π)L9 4 v0
答:(1)电场强度E的大小为
;mv02 2qL
(2)匀强磁场的磁感应强度B的大小为
,方向方向垂直纸面向里;2mv0 3qL
(3)粒子从M点进入电场,经NP点最后又回到M点所用的总时间为
.(3+
π)L9 4 v0
