问题
问答题
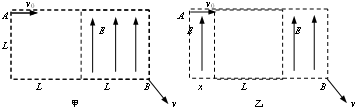
如图所示,在长为2L、宽为L的区域内有正好一半空间有场强为E、方向平行于短边的匀强电场,有一个质量为m,电量为e的电子,以平行于长边的速度v0从区域的左上角A点射入该区域,不计电子所受重力,要使这个电子能从区域的右下角的B点射出,求:
(1)无电场区域位于区域左侧一半内时,如图甲所示,电子的初速应满足什么条件?
(2)无电场区域的左边界离区域左边的距离为x时,如图乙所示,电子的初速又应满足什么条件.
答案
(1)粒子做匀速直线运动,由运动学公式可知,
无电场中运动的时间,t=L v0
在电场中做类平抛运动,由牛顿第二定律,则有L=
at2=1 2 eEL2 2m v 20
由上两式,综合解得:v0=eEL 2m
(2)粒子做匀速直线运动,则运动时间为t1=x v0
在两个电场中的偏距:y1+y3=
at2=1 2 eEL2 2m v 20
在无电场区域中的运动时间为t2,偏距y2,
运动的时间,t2=L v0
偏转位移,y2=at1t2=eELx m v 20
则有L=y1+y2+y3=eEL(
+x)L 2 m v 20
解得:v0=eE(L+2x) 2m
答:(1)无电场区域位于区域左侧一半内时,如图甲所示,电子的初速应满足 v0=
条件;eEL 2m
(2)无电场区域的左边界离区域左边的距离为x时,如图乙所示,电子的初速又应满足:v0=
条件.eE(L+2x) 2m
