问题
问答题
利用代换
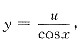 将方程y"cosx-2y’sinx+3ycosx=ex化简,并求出原方程的通解.
将方程y"cosx-2y’sinx+3ycosx=ex化简,并求出原方程的通解.
答案
参考答案:u"+4u=ex.
解析:[考点提示] 二阶变系数线性非齐次微分方程.
[解题分析] 题设所给方程为变系数方程,可由代换[*]将其化为关于u的二阶微分方程再求解.应先由[*]求得y’,y"与u’,u"的关系如下,将y=asecx两边对x求导,
得
y’=u’secx+usecx·tanx. ①
再由①式两边对x求导,得
y"=u"secx+2u’secx·tanx+usecx·tan2x+usec3x. ②
将①、②式代人原方程,得u"+4u=ex.该方程是关于u的二阶常系数线性非齐次方程,先求其相应的齐次方程的通解,由特征方程λ2+4=0求得特征值为λ1=2i,λ2=-2i,从而齐次方程通解为y=C1cos2x+C2sin2x.设方程特解为y*=Aex,代回方程u"+4u=ex,得A[*],因此[*].因此非齐次方程通解为
[*]
其中C1,C2为任意常数.
由代换[*]原方程通解为
[*]
注:本题在化简原方程时,也可由代换u=ycosx的两边对x求导,得
u’=y’cosx-ysinx. ③
再由③式两边对x求导,得
u"=y"cosx-2y’sinx-ycosx. ④
③、④式与①、②式是等价的,代入原方程都可得出同样的方程
u"+4u=ex.
