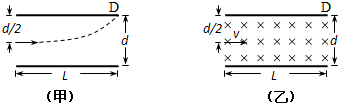
有一平行板电容器,内部为真空,两个极板的间距为d,极板长为L,极板间有一匀强电场,U为两极板间的电压,电子从极板左端的正中央以初速v0射入,其方向平行于极板,并打在极板边缘的D点,如图(甲)所示.电子的电荷量用e表示,质量用m表示,重力不计.回答下面问题(用字母表示结果).
(1)求电子打到D点的动能;
(2)电子的初速v0必须大于何值,电子才能飞出极板;
(3)若极板间没有电场,只有垂直纸面的匀强磁场,磁感应强度大小为B,电子从极板左端的正中央以平行于极板的初速v0射入,如图(乙)所示,则电子的初速v0为何值,电子才能飞出极板?
(1)设电子打到D点时的动能为Ek,由动能定理可得:
Ek-
mv02=1 2
e…①U 2
由①式解得:Ek=
e+U 2
m1 2
…②v 20
(2)设电子刚好打到极板边缘时的速度为v,电子在平行板电容器间做类平抛运动,设其在竖直方向的加速度为a,在电场中的飞行时间为t,则由电场力及牛顿第二定律、平抛运动的规律可得:
=ma…③eu d
d=1 2
at2 …④1 2
v=
…⑤L t
由③④⑤式联立解得:v=L d ue m
所以电子要逸出电容器,必有:v0>L d eu m
(3)在只有磁场情况下电子要逸出电容器,有两种情况.
①电子从左边边缘飞出磁场,做半圆周运动,其半径:R1=
d…⑥1 4
由洛仑兹力和向心力公式可得:ev1B=m
…⑦v 21 R1
由⑦式解得:v1=
…⑧eBd 4m
因此电子避开极板的条件是:v1<
…⑨eBd 4m
②电子从右边出,做半圆周运动其半径:
=L2+(R2-R 22
)2…⑩d 2
由⑩式解得:R2=4L2+d2 4d
由洛仑兹力和向心力公式可得:ev2B=m
…(11)v 22 R2
由(11)式解得:v2=
…(12)(4L2+d2)eB 4dm
电子避开极板的条件是:v2>
…(13)(4L2+d2)eB 4dm
答:(1)电子打到D点的动能是
e+U 2
m1 2
;v 20
(2)电子要飞出电容器,必有v0>L d
.ue/m
(3)电子的初速v0<
或v2>eBd 4m
时,电子才能飞出极板.(4L2+d2)eB 4dm
