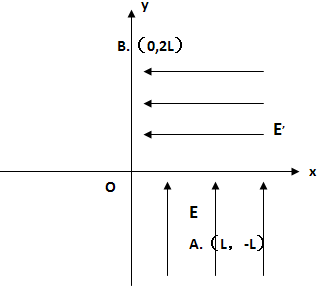
如图,质量为m、带电量为q的粒子,在第四象限匀强电场A处静止释放(不计粒子的重力),粒子经过第一象限区域的匀强电场后,恰好过y轴上的B,A点坐标为(L,-L),B点坐标为(0,2L),第四象限匀强电场为E,y轴的左侧为足够大的匀强磁场(图中未画),带电粒子恰好通过坐标原点O点,求:
(1)第一象限电场强度E;
(2)匀强磁场B的大小和方向;
(3)带电粒子从A运动到原点O时间t.

(1)设粒子从第四象限射出时的速度为v0,
粒子在第四象限做初速度为零的匀加速运动,
有:L=
at2=1 2
v0t,1 2
粒子在第一象限做类平抛运动,
竖直方向:2L=v0t′,
水平方向:L=
a′t′2,1 2
解得:t′=t,a′=a,E′=E;
(2)设带电粒子进入磁场时与y轴夹角是θ,
则tanθ=
=vx vy
=vx v0
=1,则θ=45°;a′t′ at
即带电粒子从B点和Yy轴成450进入磁场,
在洛伦兹力作用下偏转回到O点,如图:
在第四象限内,由动能定理得:qEL=
mv02-0,1 2
粒子进入磁场时的速度v=
=v0 cos45°
v0,2
在磁场中,洛伦兹力提供向心力,
由牛顿第二定律得:qvB=m
,v2 R
有图示,根据数学知识可得:R=
L,2
解得:B=
;粒子带正电,所受洛伦兹力指向圆心,2mE qL
由左手定则可知,磁感应强度垂直于纸面向下;
(3)粒子在第四象限内:L=
at2=1 2
(1 2
)2t2,qE m
则t=
,粒子在第一象限内的运动时间t′=t=2mL qE
,2mL qE
粒子在磁场中的运动时间:t″=
T=φ 2π
T=3 4
×3 4
=3π2πR v
,mL 8qE
总的时间:t总=t+t′+t″=2
+3π2mL qE
;mL 8qE
答:(1)第一象限电场强度为E;
(2)匀强磁场B的大小为
,方向垂直于纸面向下;2mE qL
(3)带电粒子从A运动到原点O时间为2
+3π2mL qE
.mL 8qE
