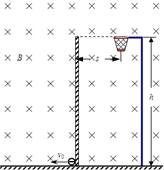
如图，水平地面上方有一绝缘弹性竖直薄档板，板高h=3m，与板等高

问题问答题

如图，水平地面上方有一绝缘弹性竖直薄档板，板高h=3m，与板等高处有一水平放置的小篮筐，筐口的中心距挡板s=1m．整个空间存在匀强磁场和匀强电场，磁场方向垂直纸面向里，磁感应强度B=1T，而匀强电场未在图中画出；质量m=1×10^-3kg、电量q=-1×10^-3C的带电小球（视为质点），自挡板下端的左侧以某一水平速度v₀开始向左运动，恰能做匀速圆周运动，若小球与档板相碰后以原速率弹回，且碰撞时间不计，碰撞时电量不变，小球最后都能从筐口的中心处落入筐中．（g取10m/s²，可能会用到三角函数值sin37°=0.6，cos37°=0.8）．试求：

（1）电场强度的大小与方向；

（2）小球运动的可能最大速率；

（3）小球运动的可能最长时间．

答案

（1）小球做匀速圆周运动，则

qE=mg

故E=

=10N/C

电场方向竖直向下

（2）若小球速率最大，则运动半径最大，

如轨迹①所示

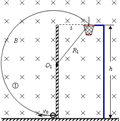
=s2+(h-R1)2

可得：R1=

由qv1B=m

⇒v1=

qBR1

m/s

（3）因为速度方向与半径垂直，圆心必在挡板所在的竖直线上．

且R≥s=1m

小球与挡板碰撞n次后落入筐中，则有

2nR＜h

⇒n＜1.5，故n可取0或1才能

保证小球落入筐中

①当n=0时，即为（2）问中的解

②当n=1时，有

（3R-h）²+s²=R²

可得R₂=1m，运动轨迹如由图中②所示

或者R3=

m，运动轨迹如由图中③所示

以轨迹③运动，小球所花时间最长

则有

2πm

=2π

sinθ=

故θ=53°，轨迹③运动对应的圆心角α=360°+（180°-53°）=487°

运动最长时间为t=

360°

974

360

πs≈8.5s

答：（1）电场强度E=10N/C，电场方向竖直向下；

（2）小球运动的可能最大速率为

m/s；

（3）小球运动的可能最长时间为8.5s．