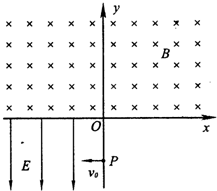
如图所示,在xOy平面内的第III象限中有沿-y方向的匀强电场,场强大小为E.只第I和第II象限有匀强磁场,磁场方向垂直于坐标平面向里,有一质量为m,电荷量为e的电子,从y轴的P点以初速度v0垂直于电场方向进入电场,P点坐标为(0,-),经电场偏转后,与x轴负半轴成一定角度进入磁场,设磁感应强度B的大小为.求:
(1)电子经过x轴负半轴的坐标和此时速度方向与-x轴方向的夹角;
(2)电子再次经过y轴负半轴的坐标.
(1)电子在电场做类平抛运动,加速度为a=
令y0=,则时间为t=
电子经过x轴负半轴的坐标x=-v0t=-v0=-2y0=-
由tanθ===1,得θ=45°
故速度方向与-x轴方向成45°
(2)电子进入磁场速度应为v0,进入磁场方向与x轴负方向成45°
进入磁场所作圆周运动半径R====y0
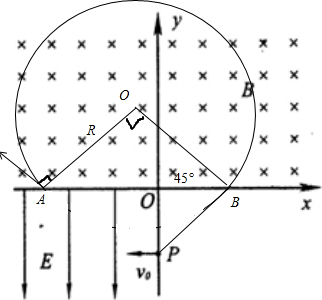
如图,由几何关系可知三角形OAB为等边直角三角形,令轨迹与x轴两交点间距离为AB,已知半径R=y0
由等边直角三角形可知=R=3y0
由(1)问中知|OA|=2y0
∴=-=3y0-2y0=y0
如图,由对称性要知:电子接着从B点射出磁场时,速度方向与x轴负方向成45°角,电子做匀速直线运动
当电子经过y轴的负半轴时,可知|OB|=|OP|即P点坐标为(0,y0)即坐标为(0,-).
故再次经过y轴的坐标为-,即与P点重合.
答:(1)电子经过x轴负半轴的坐标为(-,0)和此时速度方向与-x轴方向的夹角为45°;
(2)电子再次经过y轴负半轴的坐标(0,-).