如图甲所示,xOy位于竖直平面内,以竖直向上为y轴正方向,在y轴左侧有正交的匀强磁和匀强电场,其中匀强磁场垂直于xOY平面向里,磁感应强度为B,匀强电场方向竖直向上,电场强度为E0,在y轴右侧有竖直方向的匀强电场,场强的方向和大小都做周期性的变化,当电场方向向下时,电场强度为E1,向上时为E2,在坐标为(-R,R)处和第一象限某处有完全相同的带正电的微粒P和Q,微粒P和Q的带电荷量均为q,现以一定的速度水平向左释放微粒P,P在竖直面内恰好做匀速圆周运动,同时由静止释放Q,且只有Q每次经过x轴时,y轴右侧的电场方向才发生改变,若两微粒总是以相同的速度同时通过x轴
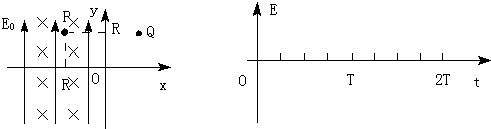
(1)求场强E1和E2的大小及其变化周期T;
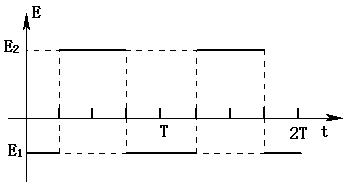
(2)在图乙中作出该电场的变化图象(以释放电荷P时作为初始时刻,竖直向上为场强的正方向),要求至少画出两个周期的图象.
(1)由于通过x轴时,两个粒子速度均是竖直方向,则P微粒运动半径为R,
得:qE0=mg,qvB=m
解得 v=v2 R BRq E0
P粒子运动的周期T0=
=2πR v 2πE0 Bg
Q粒子在
时刻以速度v向下通过x轴,则有T0 4
v=a
解得a=T0 4 2RB2 π E 20
向下运动时,根据牛顿第二定律得
mg+qE1=ma,解得 E1=
-E02RgB2 πE0
向上运动时:qE2-mg=ma
解得E2=
+E02RgB2 πE0
根据分析得到:Q在
时刻到达最低点,T0 2
T0时刻以向上的速度v通过x轴,T0时回到原出发点,速度为0,是一种往复运动,其周期为T=T0.3 4
(2)E-t图如图所示.
答:(1)场强E1=
-E0,E2=2RgB2 πE0
+E0,其变化周期T=T0;2RgB2 πE0
(2)E-t图如图所示.
