用如图所示的装置来选择密度相同、大小不同的球状纳米粒子.在电离室中使纳米粒子电离后表面均匀带正电,且单位面积的电量为q0.电离后,粒子缓慢通过小孔O1进入极板间电压为U的水平加速电场区域I,再通过小孔O2射入相互正交的恒定匀强电场、匀强磁场区域II,其中电场强度为E,磁感应强度为B、方向垂直纸面向外.收集室的小孔O3与O1、O2在同一条水平线上.已知纳米粒子的密度为ρ,不计纳米粒子的重力及纳米粒子间的相互作用.(V球=
πr3,S球=4πr2)4 3
(1)如果半径为r0的某纳米粒子恰沿直线O1O3射入收集室,求该粒子的速率和粒子半径r0;
(2)若半径为4r0的纳米粒子进入区域II,粒子会向哪个极板偏转?计算该纳米粒子在区域II中偏转距离为l(粒子在竖直方向的偏移量)时的动能;(r0视为已知)
(3)为了让半径为4r0的粒子沿直线O1O3射入收集室,可以通过改变那些物理量来实现?提出一种具体方案.
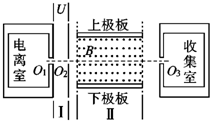
(1)半径为r0的纳米粒子在区域Ⅱ中沿直线运动,受到电场力和洛伦兹力作用
由F洛=qvB
F电=Eq
得qvB=Eq ①
v=
②E B
粒子在区域Ⅰ中加速运动,通过小孔O2时的速度为v
由动能定理 qU=
mv2③1 2
半径为r0的纳米粒子质量m=ρ×
πr3④4 3
电量q=q0×4πr2⑤
由②③④⑤式得 r0=
⑥6q0UB2 ρE2
(2)由③④⑤式得半径为r0的粒子速率v=
⑦6q0U ρr0
由⑦式判断:粒子半径为4 r0时,粒子速度v'=
,故F洛<F电,粒子向上极板偏 v 2
设半径为4r0的粒子质量m'、电量q',偏转距离为l时的动能为Ek
解法一:粒子在区域Ⅰ、Ⅱ全过程中,由动能定理Ek=q'U+q'El⑧
q′=q0×4π(4r0)2⑨
由⑧⑨式得粒子动能 Ek=64π
q0(U+El)⑩r 20
解法二:粒子在区域Ⅱ中,由动能定理 Eq′l=EK-
m′v′2q′=q0×4π(4r0)2m′=ρ×1 2
π(4r0)34 3
得 Ek=64π
q0(U+El)r 20
(3)由⑥式可知,粒子沿直线射入收集室可以通过改变电场强度E、磁感应强度B和加速电压U来实现.
只改变电场强度E,使电场强度E为原来的
,则半径为4r0的粒子受到的电场力与洛伦兹力平衡,能沿直线射入收集室.1 2
答:(1)如果半径为r0的某纳米粒子恰沿直线O1O3射入收集室,则该粒子的速率为
,粒子半径r0=E B
;6q0UB2 ρE2
(2)若半径为4r0的纳米粒子进入区域II,粒子向上极板偏.该纳米粒子在区域II中偏转距离为l(粒子在竖直方向的偏移量)时的动能为Ek=64π
q0(U+El).r 20
(3)为了让半径为4r0的粒子沿直线O1O3射入收集室,可以只改变电场强度E,使电场强度E为原来的
,则半径为4r0的粒子受到的电场力与洛伦兹力平衡,能沿直线射入收集室.1 2
