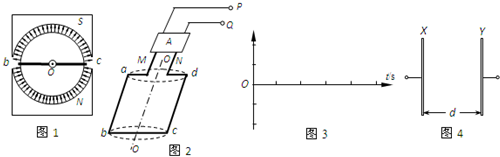
某种小发电机的内部结构平面图如图1所示,永久磁体的内侧为半圆柱面形状,它与共轴的圆柱形铁芯间的缝隙中存在辐向分布、大小近似均匀的磁场,磁感应强度B=0.5T.磁极间的缺口很小,可忽略.如图2所示,单匝矩形导线框abcd绕在铁芯上构成转子,ab=cd=0.4m,bc=0.2m.铁芯的轴线OO′在线框所在平面内,线框可随铁芯绕轴线转动.将线框的两个端点M、N接入图中装置A,在线框转动的过程中,装置A能使端点M始终与P相连,而端点N始终与Q相连.现使转子以ω=200π rad/s角速度匀速转动.在图1中看,转动方向是顺时针的,设线框经过图1位置时t=0.(取π=3)
(1)求t=
s时刻线框产生的感应电动势;1 400
(2)在图3给出的坐标平面内,画出P、Q两点电势差UPQ随时间变化的关系图线(要求标出横、纵坐标标度,至少画出一个周期);
(3)如图4所示为竖直放置的两块平行金属板X、Y,两板间距d=0.17m.将电压UPQ加在两板上,P与X相连,Q与Y相连.将一个质量m=2.4×10-12kg,电量q=+1.7×10-10C的带电粒子,在t0=6.00×10-3s时刻,从紧临X板处无初速释放.求粒子从X板运动到Y板经历的时间.(不计粒子重力)
(1)根据法拉第电磁感应定律知:感应电动势 E=BSω=B×ab×bc×ω
代入数据得 E=24V
(2)由题意知线框转过π弧度电势将反向,根据右手定则知,开始时P点电势低即UPQ=-24V,电势反向时间为
t=
=0.005s,所以图象为:π ω

(3)粒子开始运动后一个周期内的运动示意图如图所示
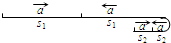
粒子在电导中产生的加速度大小为:a=Uq dm
向Y板加速的距离 s1=
a×(T-t0)2=0.08m 1 2
向X板加速的距离 s2=
a×(t0-1 2
T)2=0.005m 1 2
一个周期内前进的距离 S=2S1-2S2=0.15m
由于S<d,d-S=0.02m<S1,所以粒子将在下一周期向Y板加速过程中到达Y板
设这次加速时间为t d-s=
at2t=2.0×10-3s 1 2
求出总时间 t总=T+t=1.2×10-2s
答:(1)感应电动势为24V
(2)图象见上图;
(3)粒子经历时间为1.2×10-2s
