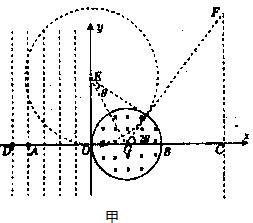
如图所示,平面直角坐标系xoy内,在x≤0的区域内分布着匀强电场,其等势线如图中虚线所示(相邻等势面间的距离相等).在A点源源不断的产生速率为零、质量为m、电荷量为+q的粒子,经电场加速后从O点进入一个圆形的匀强磁场区,其磁感应强度为B,方向垂直纸面向里,其半径为R,直径OB在x轴上.在x=4R处有一个垂直x轴很大的光屏,与x轴的交点为C,粒子打在光屏上可出现亮点.设粒子的重力不计,A点所在的等势面电势为零,D点的电势为
.B2R2q 2m
(1)求从A点产生的粒子经电场和磁场后,打在光屏上的位置.
(2)若将圆形磁场区以O点为轴,整体逆时针将OB缓慢转过90度角(与y轴重合),求此过程中粒子打在光屏上的点距C点的最远距离.

A与O间的电势差U=4UDA=4×
=B2R2q 2m
,2B2R2q m
粒子经过电场加速过程中,由动能定理得:qU=
mv2-0,1 2
解得:v=
,2qBR m
粒子进入磁场做圆周运动轨道半径为r,
由牛顿第二定律:qvB=
,解得:r=2R,mv2 r
粒子运动轨迹如图甲所示,粒子做圆周运动的圆心角为2θ,
由几何关系得:tanθ=
=R r
,tan2θ=1 2
,CF 3R
tan2θ=
=2tanθ 1-(tanθ)2
,解得:CF=4R,4 3
故所以F点的坐标为(4R,4R);
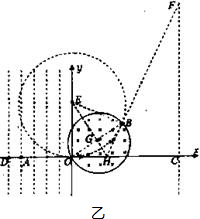
(2)当圆形磁场旋转时,粒子做圆周运动的圆心和轨迹都不变,
当粒子在磁场中对应的弦长为直径时对应的坐标最大打到距离c点最远处如图乙所示,
由图中几何关系得:R=rsinβ,tan2β=
,解得:CF=(4CF 3R
-2)R;3
答:(1)从A点产生的粒子经电场和磁场后,打在光屏上的位置坐标为(4R,4R);
(2)粒子打在光屏上的点距C点的最远距离为(4
-2)R.3
