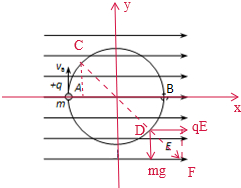
如图所示,一绝缘细圆环半径为 r,其环面固定在竖直平面上,方向水平向右、场强大小为E的匀强电场与圆环平面平行,环上穿有一电荷量为+q 的小球,可沿圆环做无摩擦的圆周运动,若小球经A点时速度方向恰与电场方向垂直,且圆环与小球间沿水平方向无力的作用.小球沿顺时针方向运动,且qE=mg,求小球运动到何处时,对环的作用力最大?最大作用力为多大?
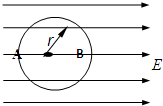
由题意可知小球到达A点时电场力提供向心力即qE=mv 2A r
,①
由qE=mg.由于球只受到重力和电场力的作用,并且重力和电场力的大小相等,当两个力的合力沿半径向外时,如图所示经过D点时,动能最大,环对球的作用力最大,此时CD与竖直方向的夹角为45°,根据动能定理得:
从A→D:mgrcos45°+qE(1+sin45°)r=
m1 2
-v 2D
m1 2
②v 2A
根据牛顿第二定律得:N-
mg=m2
③v 2D r
联立①②③得:N=3(1+
)mg2
由牛顿第三定律得知:小球对环的最大作用力N′=N=3(1+
)mg.2
答:当小球运动到图是D点,CD与竖直方向的夹角为45°时,对环的作用力最大,最大作用力为3(1+
)mg.2
