问题
问答题
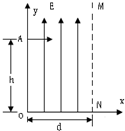
在空间中取坐标系xoy,在第一象限内平行于y轴的虚线MN与y轴距离为d,从y轴到MN之间的区域充满一个沿y轴正方向的匀强电场,场强大小为E,如图所示.初速度可以忽略的电子经过另一个电势差为U的电场加速后,从y轴上的A点以平行x轴的方向射入第一象限区域,A点坐标为(0,h).已知U>
,不计电子的重力影响,求电子经过x轴时的位置.Ed2 4h
答案
设电子的电量为e、质量为m,
电子经过电势差为U的电场加速后获得速度v0,
由动能定理得:eU=
m1 2
-0,v 20
电子在电场中做类平抛运动,设电子在匀强电场中运动的时间为t、加速度为a,
离开电场时在电场方向上的偏移量为y、获得的速度为vy,
水平方向:d=v0t,
由牛顿第二定律得:eE=ma,
在竖直方向:y=
at2,竖直分速度:vy=at,1 2
解得U=
,因为U>Ed2 4y
,所以y<h,说明电子离开电场后才经过x轴.Ed2 4h
设电子离开电场后经过时间t'到达x轴,在x轴方向上的位移为x',
x′=v0t′,y′=h-y=vyt′,
电子经过轴时与原点O的距离L=d+x′,
由以上各式解得:L=
+d 2
;2hU Ed
答:电子经过x轴时的位置为x=
+d 2
;2hU Ed
