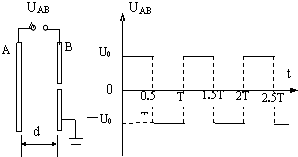
如图中A和B表示在真空中相距为d的两平行金属板加上电压后,它们之间的电场可视为匀强电场;右边表示一周期性的交变电压的波形,横坐标代表时间t,纵坐标代表电压UAB,从t=0开始,电压为给定值U0,经过半个周期,突然变为-U0….如此周期地交替变化.在t=0时刻将上述交变电压UAB加在A、B两极上,电子质量为m,电量为e,求:
(1)在t=0时刻,在B的小孔处无初速地释放一电子,要想使这电子到达A板时的速度最大,则所加交变电压的频率最大不能超过多少?
(2)在t=0时刻,在B的小孔处无初速地释放一电子,要想使这电子到达A板时的速度最小(零),则所加交变电压的频率为多大?
(3)在t=?时刻释放上述电子,在一个周期时间,该电子刚好回到出发点?
试说明理由并讨论物理量间应满足什么条件.
(1)要求电子到达A板的速度最大,则电子应该从B板一直加速运动到A板,即电子从B板加速运动到A板所用时间必须满足:
t≤
①T 2
依题意得,s=
×1 2
×t2=d ②eU md
f=
.1 T
综合①②可得:f≤eU0 8md2
(2)由电子在电场中运动时的受力情况及速度变化情况可知:要求电子到达A板的速度为零,则电子应该在t=nT(n=1,2,3,…)时刻到达A板,电子在每个
内通过的位移为:T 2
S=
×1 2
×(eU0 md
)2③T 2
依题意知:d=n(2S) ④
综合③、④可得:f=
(n=1,2,3,…).neU0 4md2
(3)在t=nT+
时刻释放电子,经过一个周期,在t=T 4
时刻,电子刚回到出发点.条件是在半个周期即从(5T 4
~T 4
)时间内,电子的位移小于d,3T 4
有:d=2×1 2
(eU md
)2,f=T 4 1 T
亦即频率f≥
.eU 16md2
答:(1)在t=0时刻,在B的小孔处无初速地释放一电子,要想使这电子到达A板时的速度最大,则所加交变电压的频率最大不能超过
.eU0 8md2
(2)在t=0时刻,在B的小孔处无初速地释放一电子,要想使这电子到达A板时的速度最小(零),则所加交变电压的频率为f=
(n=1,2,3,…).neU0 4md2
(3)在t=nT+
时刻释放电子,经过一个周期,电子刚回到出发点.f≥T 4
.eU 16md2