搜题请搜索小程序“爱下问搜题”
问题 问答题

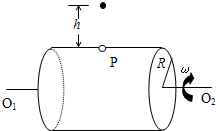
如图所示，一个水平放置的圆桶绕水平轴O1O2匀速转动，桶的半径R=2m，桶壁很薄，壁上有一小圆孔P，当圆孔运动到桶的正上方时，在孔的正上方h=3.2m处有一个小球由静止开始下落，已知圆孔的半径略大于小球的半径．试求：要使小球在整个下落过程中都不与桶壁碰撞，圆桶转动的角速度的所有可能值．

答案

设小球下落h所用时间t1，经过圆桶所用时间为t2，则h=

1
2
gt2

解得t1=0.8 s

h+2R=

1
2
g（t1+t2）2

解得t2=0.4 s

设圆桶的运动周期为T，故有：

nT=t1（n=1，2，3，…）

（m-

1
2
）T=t2    （m=1，2，3，…）

解得：T=

0.8
n
 （n=1，2，3，…）

且T=

0.8
2m-1
   （m=1，2，3，…）

故T=

0.8
2m-1
（m=1，2，3，…）

角速度为：ω=

2π
T
=2.5π（2m-1）（m=1，2，3，…）

答：要使小球在整个下落过程中都不与桶壁碰撞，圆桶转动的角速度的可能值为：ω=

2π
T
=2.5π（2m-1）（m=1，2，3，…）．

实验题

请根据图所示的实验装置图回答

（1）指出图中标有数字的仪器的名称：① _________ ，② _________ ，③ _________ ．

（2）在实验室用高锰酸钾制氧气时，试管口的棉花团的作用是 _______________ ．

（3）当用B装置制取氧气时，仪器②内盛放的液体是 _________ ，写出反应的文字（或符号）表达式： _________ ．

（4）做铁丝在氧气中燃烧的实验时应该在集气瓶底放上 _________ 或 _________ ，目的是 _________ ．

（5）铁丝在氧气中燃烧的现象是 ____________ ；硫在氧气中燃烧的现象是 _________ ；红磷在空气中燃烧的现象是 ___________________

（6）实验室常用氯化铵固体与碱石灰固体共热来制取氨气．常温下氨气是一种无色、有刺激性气味的气体，密度比空气小，氨气极易溶于水．制取氨气反应的文字表达式：氯化铵+熟石灰氯化钙+氨气+水．则制取并收集氨气，应该从上图中选择的发生装置是_________（填序号），收集装置是_________（填序号）．

（7）在实验室制取并收集二氧化碳可选用______________（填字母编号），写出实验室制取二氧化碳反应的文字（或符号）表达式：_______________．
查看答案
问答题 简答题

炉子砌体的维护有哪些（写出其中3点）？
查看答案