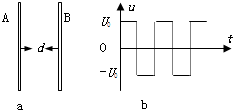
如图(a)所示,A和B表示在真空中两平行金属板,加上电压后,它们之间的电场可视为匀强电场,图(b)表示一周期性的交变电压波形,横坐标代表时间t,纵坐标代表电压U,从t=0开始,电压为一给定值U0,经过半个周期,突然变为-U0,再过半个周期,又突然变为U0;…如此周期性交替变化.将上述交变电压U加在A、B两板上,使开始时A板电势比B板高.在t=0时,在紧靠B板处有一个初速为零的电子(质量为m,电量为q)在电场作用下开始运动,经过时间T(T为电压变化的周期且已知)刚好到达A板.
(1)求两板间的距离d;
(2)在t=
时,在紧靠B板处有一个初速为零的电子在电场作用下开始运动,则电子经过多长时间打在哪个板上?T 3
(3)在t=
时,在紧靠B板处有一个初速为零的电子在电场作用下开始运动,则电子经过多长时间打在哪个板上?T 6
(1)由于前后两个半周期电压大小相等,故电子在极板间的加速a=
大小相等,又初末速度为零,故全程的平均速度相等,则加速阶段和减速度阶段的位移相等:qU md
d=1 2
(qU0 md
)2×2T 2
解得:
d=T 2 qU0 m
(2)在t=
时,初速为零的电子,由于加速时间小于减速时间,故会打到B板上,经过时间t=T 3
×2+t1打在B板上.T 6
其中t1满足:
a(1 2
)2×2=T 6
a1 2 t 21
解得:
t1=
T2 6
故:
t=
T2+ 2 6
(3)在t=
时,初速为零的电子,经过时间T向A的位移为:T 6
s=[
a(1 2
)2-T 3
a(1 2
)2]×2=T 6
aT21 12
经分析电子到达A板的时间应为:
t=(2+
)T-t22 3
其中t2满足:
a(1 2
)2×2-T 3
aT2=1 12
a1 2 t 22
解得:
t2=
T2 6
故:
t=
T16- 2 6
答:
(1)两板间的距离d=T 2
;qU0 m
(2)在t=
时,在紧靠B板处有一个初速为零的电子在电场作用下开始运动,则电子经t=T 3
T打在B板上.2+ 2 6
(3)在t=
时,在紧靠B板处有一个初速为零的电子在电场作用下开始运动,则电子经t=T 6
T打在A板上.16- 2 6
