问题
问答题
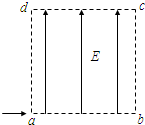
如图所示，边长为L的正方形区域abcd内存在着匀强电场．电量为q、动能为E0的带电粒子从a点沿ab方向进入电场，不计重力．
（1）若粒子从c点离开电场，求电场强度的大小和粒子离开电场时的动能．
（2）若粒子离开电场时动能为EK′，求电场强度的大小？
答案
（1）粒子的初动能为，E0=
| 1 |
| 2 |
| v | 20 |
粒子在ab方向上作匀速运动，L=v0t
粒子在ad方向上做初速度为0的匀加速运动，L=
| 1 |
| 2 |
根据牛顿第二定律，a=
| qE |
| m |
所以E=
| 4E0 |
| qL |
根据动能定理，有
qEL=Ekt-E0
所以
Ekt=qEL+E0=5E0．
即电场强度的大小为
| 4E0 |
| qL |
（2）根据牛顿第二定律，有
qE=ma ①
沿初速度方向做匀速运动，有
x=v0t ②
沿电场方向的分位移为
y=
| 1 |
| 2 |
根据动能定理，有
qEy=EK′-E0 ④
当带电粒子从bc边飞出时，x=L，y＜L，由①②③④式联立解得
E=
v0
| ||
| qL |
| ||
| qL |
当带电粒子从cd边飞出时，y=L，x＜L，由①②③④式联立解得
E=
| Ek′-E0 |
| qL |
即当带电粒子从bc边飞出时电场强度为E=
| ||
| qL |
| Ek′-E0 |
| qL |
