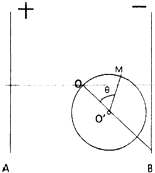
两块竖直放置足够长的带电平行金属板A、B,相距d=1.0m,两板间电势差UAB=2500V,O点到两板的距离相等.在O点有一粒子源,释放质量m=2.5×10-3kg、电量q=1.0×10-5C的带正电微粒.过O点以半径R=0.25m作一个圆,圆心O′在过D点向右下方倾斜45°的直线上.M在圆周上.∠OO′M=θ=60°.不计粒子间的相互作用,取g=10m/s2:
(1)求带电微粒在金属板间运动的加速度大小;
(2)若某带电微粒初速度大小为v0=2.0m/s,与水平方向成45°角斜向左上方,试通过计算判断该微粒打在哪个极板上;
(3)若某一微粒在O点射出时初速度方向与水平方向成45°角斜向右上方,且经过一段时间通过M点,求该微粒通过M点时的动能.
(1)带电微粒在复合场中受到重力和电场力的作用,受力如图,则:
FE=Eq=2500×1.0×10-5N=2.5×10-2N
G=mg=2.5×10-3×10N=2.5×10-2N
合力:F=
=2.5
+G2F 2E
×10-2N2
由牛顿第二定律得:F=ma
所以:a=
=F m
m/s2=102.5
×10-22 2.5×10-3
m/s22
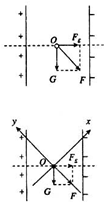 方向与水平方向成45°角斜向右下.
方向与水平方向成45°角斜向右下.
(2)如图所示微粒射出后,沿y方向做匀减速直线运动,
在y方向是最大位移:ym=
=v 20 2a
m2 10
如图所示,从O沿y轴到金属板的距离为:Y=
d=2 2
m2 2
由于ym<Y,微粒的速度减小到0后将反向加速,最后打到右侧的金属板上.
(3)微粒在O点射出时初速度方向与水平方向成45°角斜向右上方,则微粒做类平抛运动,则:
Rsinθ=v0t
R-Rcosθ=
at21 2
解得:v0=
=gRsin2θ
(1-cosθ)2
(1+cosθ)5 2 4
微粒从O点出发时的动能:EKO=
m1 2
=v 20
mg(1+cosθ)2 16
到达M点时的动能:
EKM=
mgR(1-cosθ)+2
m1 2
=v 20
mg(5-3cosθ)=2 16
×2.5×10-3×10×(5-3×cos60°)=7.7×10-3J2 16
答:(1)带电微粒在金属板间运动的加速度大小是10
m/s;2
(2)若某带电微粒初速度大小为v0=2.0m/s,与水平方向成45°角斜向左上方,微粒打在右侧极板上;
(3)若某一微粒在O点射出时初速度方向与水平方向成45°角斜向右上方,该微粒通过M点时的动能是7.7×10-3J.
