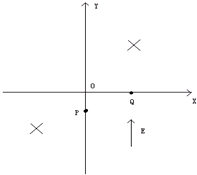
如图，在坐标系xoy的第一、第三象限内存在相同的匀强磁场，磁场方向垂直于xoy面向里；第四象限内有沿y轴正方向的匀强电场，电场强度大小为E．一质量为m、带电量为+q的粒子自y轴的P点沿x轴正方向射入第四象限，经x轴上的Q点进入第一象限，随即撤去电场，以后仅保留磁场．已知OP=d，OQ=2d，不计粒子重力．
（1）求粒子过Q点时速度的大小和方向．
（2）若磁感应强度的大小为一定值B0，粒子将以垂直y轴的方向进入第二象限，求B0；
（3）若磁感应强度的大小为另一确定值，经过一段时间后粒子将再次经过Q点，且速度与第一次过Q点时相同，求该粒子相邻两次经过Q点所用的时间．
（1）设粒子在电场中运动的时间为t0，加速度的大小为a，粒子的初速度为v0，过Q点时速度的大小为v，沿y轴方向分速度的大小为vy，速度与x轴正方向间的夹角为θ，由牛顿第二定律得qE=ma ①
由运动学公式得d=
a1 2
②t 20
2d=v0t0 ③
vy=at0 ④
v=
⑤
+v 20 v 2y
tanθ=
⑥vy v0
联立①②③④⑤⑥式得v=2
⑦qEd m
θ=45° ⑧
（2）设粒子做圆周运动的半径为R1，粒子在第一象限的运动轨迹如图，O1为圆心，由几何关系可知△O1OQ
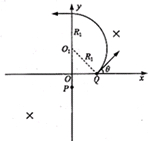为等腰直角三角形，得R1=2
d ⑨2
由牛顿第二定律得qvB0=m
⑩v2 R1
联立⑦⑨⑩式得B0=
（11）mE 2qd
（3）设粒子做圆周运动的半径为R2，由几何分析（粒子运动的轨迹如图，O2、O'2是粒子做圆周运动的圆心，Q、F、G、H是轨迹与两坐标轴的交点，连接O2、O'2，由几何关系知，O2FGO'2和O2QHO'2均为矩形，进而知FQ、GH均为直径，QFGH也是矩形，又FH⊥GQ，可知QFGH是正方形，△QOG为等腰直角三角形）可知，粒子在第一、第三象限的轨迹均为半圆，得2R2=2
d （12）2
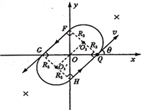粒子在第二、第四象限的轨迹为长度相等的线段，得FG=HQ=2R2 （13）
设粒子相邻两次经过Q点所用的时间为t，则有t=
（14）FG+HQ+2πR2 v
联立⑦（12）（13）（14）得
t=(2+π)2md qE
答：（1）粒子过Q点时速度的大小为v=2
．qEd m
（2）B0的大小为B0=
．mE 2qd
（3）该粒子相邻两次经过Q点所用的时间t=(2+π)
．2md qE