问题
问答题
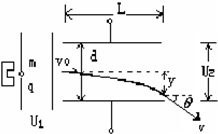
如图所示,离子发生器发射出一束质量为m,带电量为q的离子(初速度不计,重力不计),经加速电压U1加速后以垂直于电场方向射入两平行板中央,受偏转电压U2作用后,飞出电场.已知平行板的长度为L,两板间距离为d,试计算:
(1)偏转量y是多少?
(2)离子离开电场时的速度偏角θ的正切值是多大?
答案
(1)离子在加速电场中运动的过程中,只有电场力做功W=qU,根据动能定理得:qU1=
mv021 2
解得:v0=2qU1 m
离子在偏转电场中做类平抛运动,水平方向匀速直线运动
所以:L=v0t
解得:t=
=L v0
=LL 2qU1 m m 2qU1
偏转电场的场强:E=U2 d
则离子所受的电场力:F=qE=qU2 d
根据牛顿第二定律:qE=ma
解得:a=qU2 md
离子在偏转电场中做类平抛运动,竖直方向初速度为零的匀加速直线运动:
所以:y=
at2=1 2
×1 2
×(LqU2 md
)2=m 2qU1 L2U2 4dU1
(2)竖直方向上的速度vy=at=
×qU2 md L v0
所以离子离开偏转电场时的偏转角θ的正切值tanθ=
=vy v0 qU2L dm v 20
又因为qU1=
mv021 2
联立解得:tanθ=LU2 2dU1
答:(1)偏转量y是
.(2)离子离开电场时的速度偏角θ的正切值是L2U2 4dU1
.LU2 2dU1
