如图所示,带电平行金属板相距为2R,在两板间半径为R的圆形区域内有垂直纸成向里的匀强磁场,磁感应强度为B,两板及其左侧边缘连线均与磁场边界刚好相切.一质子(不计重力)沿两板间中心线O1O2从左侧O1点以某一速度射入,沿直线通过圆形磁场区域,然后恰好从极板边缘飞出,在极板间运动时间为t0.若仅撤去磁场,质子仍从O1点以相同速度射入,经
时间打到极板上.t0 2
(1)求两极板是电压U;
(2)求质子从极板间飞出时的速度大小;
(3)若两极板不带电,保持磁场不变,质子仍沿中心线O1O2从O1点射入,欲使质子从两板左侧间飞出,射入的速度应满足什么条件?
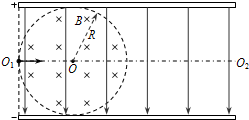
(1)设粒子从左侧O1点射入的速度为v0,极板长为L
粒子在初速度方向上做匀速直线运动L:(L-2R)=t0:
,t0 2
解得:L=4R
在电场中:L-2R=v0•t0 2
由牛顿第二定律,a=qE m
又R=
a(1 2
)2t0 2
在复合场中作匀速运动:q
=qv0BU 2R
解得v0=
,4R t0
则有,U=8R2B t0
(2)质子从极板间飞出时的沿电场方向分速度大小,vy=
t=qE m
=v02R t
从极板间飞出时的速度大小v=
=
+v 20 v 2y
v0=2 4
R2 t0
(3)设质子在磁场中做圆周运动的轨迹半径为r,质子恰好从上极板左边缘飞出时速度的偏转角为α,
由几何关系可知,β=π-α=45°,
r+
r=R2
因为R=1 2
(qE m
)2,t0 2
所以
=qE m
=qv0B m 8R t 20
根据向心力公式,qvB=m
,v2 r
解得:v=
R2(
-1)2 t0
所以质子两板左侧间飞出的条件为0<v<
R;2(
-1)2 t0
答:(1)两极板是电压U=
;8R2B t0
(2)质子从极板间飞出时的速度大小
;4
R2 t0
(3)射入的速度应满足0<v<
R条件.2(
-1)2 t0