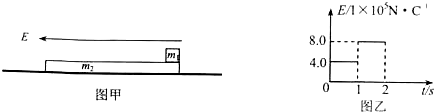
如图甲所示,质量为m2=1kg的绝缘板静止在粗糙水平地面上,质量为m1、带电量q=+1×10-5C、大小可以忽略的滑块静止在绝缘板的右端,已知滑块与绝缘板之间的动摩擦因数为μ1=0.4,绝缘板与地面之间的动摩擦因数为μ2=0.1,设最大静摩擦力等于滑动摩擦力,滑块相对绝缘板滑动过程中其电量不变,取g=10m/s2.现在该系统所在空间加一方向水平向左、大小如图乙所示变化的匀强电场,2s末撤去匀强电场后,再经时间t滑块相对绝缘板静止.
求:(1)时间t;
(2)绝缘板的长度L至少为多长,滑块才不会掉下绝缘板.
:(1)带电滑块在匀强电场中所受电场力
F=Eq ①
依题意滑块与绝缘板间的滑动摩擦力:
f1=μ1m1g=4N ②
绝缘板与地面间的滑动摩擦力:
f2=μ2(m1+m2)g=2N ③
若滑块与绝缘板间恰好无相对滑动
对整体:F-f2=(m1+m2)a ④
对滑块:F-f1=m1a ⑤
解得:F=6N a=1m/s2
即F≤6N时滑块与绝缘板间无相对滑动.
第1s内 F=Eq=4N≤6N,滑块与绝缘板间无相对滑动.
第1s末滑块、绝缘板的速度,
v0=at1=1m/s ⑦
第2s内 F=Eq=8N≥6N,滑块与绝缘板间有相对滑动.
对滑块:F-f1=m1a1 ⑧
对绝缘板:f1-f2=m2a2 ⑨
解得:a1=4m/s2,a2=2m/s2,⑩
第2s末滑块与绝缘板的速度分别为:
v1=v0+a1t2=5m/s v2=v0+a2t2=3m/s
2s末撤去匀强电场后
对滑块:-f1=m1a1′(11)
解之得:a1′=-4m/s2 (12)
经时间t滑块相对绝缘板静止时,有
v1+a1′t=v2+a2t (13)
解之得:t=
s (14)1 3
(3)在(1s+
s)=1 3
s内4 3
滑块的位移:x1=(v0t2+
a11 2
)+(v1t+t 22
a′1t2)=1 2
m (15)40 9
绝缘板的位移:x2=v0(t2+t)+
a2(t2+t)2=1 2
m (16)28 9
所以绝缘板的长度 L=x1-x2=
m (17)4 3
答:(1)时间t是
s;(2)绝缘板的长度L至少为1 3
m,滑块才不会掉下绝缘板.4 3
