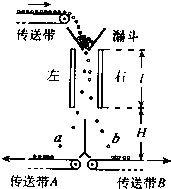
如图是某种静电分选器的原理示意图,两个竖直放置的平行金属板带有等量异号电荷,形成匀强电场.分选器漏斗的出口与两板上端处于同一高度,到两板距离相等.混合在一起的a、b两种颗粒从漏斗出口下落时,a种颗粒带上正电,b种颗粒带上负电.经分选电场后,a、b两种颗粒分别落到水平传送带A、B上.
已知两板间距d=0.1m,板的长度l=0.5m,电场仅局限在平行板之间;各颗粒所带电量大小与其质量之比均为1×10-5C/kg.设颗粒进入电场时的初速度为零,分选过程中颗粒大小及颗粒间的相互作用不计.要求两种颗粒离开电场区域时,不接触到极板但有最大偏转量.重力加速度g取10m/s2.
(1)左右两板各带何种电荷?两极板间的电压多大?
(2)若两带电平行板的下端距传送带A、B的高度H=0.3m,颗粒落至传送带时的速度大小是多少?
(3)设颗粒每次与传送带碰撞反弹时,沿竖直方向的速度大小为碰撞前竖直方向速度大小的一半.写出颗粒第n次碰撞反弹高度的表达式.并求出经过多少次碰撞,颗粒反弹的高度小于0.01m.
(1)由于a颗粒带正电,故电场方向向左,所以左板带负电荷,右板带正电荷
依题意,颗粒在平行板的竖直方向上做自由落体运动,故满足l=gt2…①
在水平方向上做匀加速直线运动,故满足s==t2…②
①②两式联立得两极板间的电压U==1×104V
(2)根据动能定理,颗粒落到水平传送带上满足qU+mg(l+H)=mv2
解得颗粒落到水平传送带上时的速度大小为v==4m/s
(3)在竖直方向颗粒作自由落体运动,根据vy2=2g(l+H)
可得颗粒第一次落到水平传送带上沿竖直方向有vy==4m/s
故颗粒第一次反弹的速度大小为,
所以根据v2=2gh可得颗粒第一次反弹高度 h1==()()
根据题设条件,颗粒第n次反弹后上升的高度hn=()n()=()n×0.8m
要hn<0.01,即()n<=,
故只有当n=4时,hn<0.01m.