问题
问答题
小李家的一个水龙头拧不紧,水一滴一滴不停地滴落到地上.小李发现,第一滴水碰地的同时,第二滴水刚好从水龙头处下落.他为了测算水滴下落的平均速度,找来了秒表和卷尺.首先量出水龙头口离地面的高度h,再用秒表计时.当他听到某一水滴滴在地上声音的同时,开启秒表开始计时,并数“1”,以后每听到一声水滴声,依次数“2、3…”,一直数到“n”时,按下秒表停止计时,读出秒表的示数为t.
(1)水滴在空中运动的平均速度的表达式为______;
(2)测得
| 次数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 高度h(m) | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.8 |
| 平均速度v(m/s) | 0.97 | 1.19 | 1.38 | 1.54 | 1.68 | 1.95 |
(3)小李为了进一步找出水滴下落的平均速度和下落高度的关系,又做了以下实验:找来一块挡板,让水滴落在挡板上.改变挡板和水龙头口之间的距离h,并仔细调节水龙头滴水的快慢,使得总是在前一滴水滴到挡板上的同时,后一滴水刚好开始下落.计时方法仍和上面一样.他从实验中又获得了如下表所示的6组数据(连同上面的一组共有7组数据).请选取合适的坐标轴,标上数据和单位,作出相应的图象,并根据图象写出平均速度和下落高度的函数关系为______.
答案
(1)n滴水所经过的路程为s=(n-1)h,水滴的平均速度
=. v
=s t
;(n-1)h t
(2)代入数据,有:
=. v
=s t
=(n-1)h t
≈2.18m/s;(20-1)×1 8.7
(3)先得到速度的平方,如下表所示;
| 次 数 | 1 | 2 | 3 | 4 | 5 | 6 |
| 高度h(m) | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.8 |
| 平均速度(m/s) | 0.97 | 1.19 | 1.38 | 1.54 | 1.68 | 1.95 |
| 平均速度平方(m2/s2) | 0.94 | 1.42 | 1.90 | 2.37 | 2.82 | 3.80 |
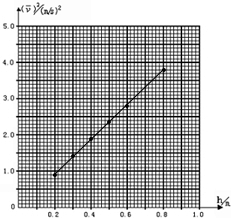
从图象上可以看出,水滴在空中运动平均速度的平方(
)2与下落高度h成正比;. v
斜率为:k=△(
)2. v △h
≈4.83.8-0.94 0.8-0.2
故表达式为:(
)2=4.8h;. v
故答案为:(1)
;(2)2.18;(3)如图所示,((n-1)h t
)2=4.8h.. v
