问题
问答题
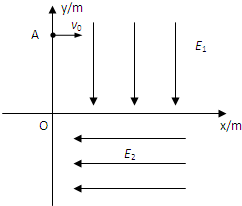
如图所示,y轴在竖直方向,x轴在水平方向,一质量为m,带电量为q的小球在座标为(0,0.3)A点以初速度v0平行于x轴正方向射入电场中,在y>0,x>0的空间存在沿y轴负方向的匀强电场E1,在y<0,x>0的空间存在沿x轴负方向的匀强电场E2,其中m=0.1kg,q=+1.0×10-3C,v0=2m/s,E1=103N/C,E2=
×103N/C,重力加速度g=10m/s2,求:3
(1)小球到达x轴上的速度;(2)小球回到y轴时的座标.
答案
(1)小球做类平抛运动,设在竖直方向加速度为a1,运动时间为t,未速度为v,v与x轴正方向夹角α
由牛顿第二定律,则有:F1=Eq+mg=ma1
位移与时间关系,h1=
a11 2 t 21
速度与时间关系,vy=a1t1
因v0=2m/s
则有,v=
+v 20 v 2y
所以tanα=vy v0
由以上各式得v=4m/s,α=60°
(2)由受力分析可知小球再次做类平抛运动,
设运动的加速度为a2,x1为第一次水平方向的位移,运动轨迹如图所示:
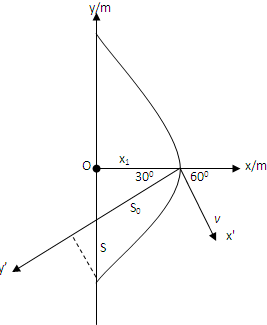
则有,a2=(qE2)2+(mg)2 m
且s0=x1 cos30°
又x1=v0t1
所以s0+
=s 2
a21 2 t 22
解
s=4t23 2
且y=s+x1tan30°
由以上各式可解得:y=1.8m
则y由上的坐标为:(0,-1.8 )
答:(1)小球到达x轴上的速度大小4m/s,与x轴正方向夹角为60°;
(2)小球回到y轴时的坐标:(0,-1.8 ).
