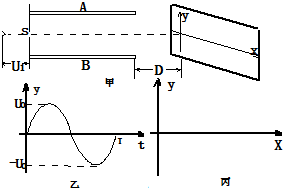
示波器的核心部分为示波管,如图中甲所示,真空室中电极K发出电子(初速不计),经过电压为U1的加速电场后,由小孔S沿水平金属板A、B间的中心线射入板中.板长L,相距为d,在两板间加上如图乙所示的正弦交变电压,前半个周期内B板的电势高于A板的电势,电场全部集中在两板之间,且分布均匀.在每个电子通过极板的极短时间内,电场可看作恒定的.在两极板右侧且与极板右端相距D处有一个与两板中心线垂直的荧光屏,中心线正好与屏上坐标原点相交.当第一个电子到达坐标原点O时,使屏以速度v沿-x方向运动,每经过一定的时间后,在一个极短时间内它又跳回到初始位置,然后重新做同样的匀速运动.(已知电子的质量为m,带电量为e,不计电子重力).求:
(1)电子进入A、B板时的初速度;
(2)要使所有的电子都能打在荧光屏上,图乙中电压的最大值U0需满足什么条件?
(3)要使荧光屏上始终显示一个完整的波形,荧光屏必须每隔多长时间回到初始位置?计算这个波形的峰值和长度.在如图丙所示的x-y坐标系中画出这个波形.
(1)电子在加速电场中运动,据动能定理有:
eU1=
m1 2
,得 v1=v 21
.2eU1 m
(2)因为每个电子在板A、B间运动时,电场可看作恒定的,故电子在板A、B间做类平抛运动,在两板之外做匀速直线运动打在屏上.
在板A、B间沿水平方向运动时有L=vlt
竖直方向有y′=
at2,且a=1 2 eU md
联立解得电子通过电场后偏转距离为 y′=eUL2 2md v 21
设偏转电压最大值为U0,则ym′=
<eU0L2 2md v 21 d 2
得 U0<2d2U1 L2
(3)要保持一个完整波形,需每隔周期T回到初始位置.
设某个电子运动轨迹如图2所示,有 tanθ=
=v2 v1
=eUL md v 21
,y′ L′
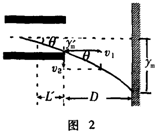
又知y′=
,联立得L′=eUL 2md v 21 L 2
由相似三角形的性质得
=
+DL 2 L 2 ym ym′
则峰值ym=L+2D L
=y ′m
.(L+2D)LU0 4dU1
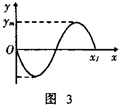
波形长度为x1=vT波形如图3所示
答;
(1)电子进入A、B板时的初速度为
;2eU1 m
(2)要使所有的电子都能打在荧光屏上,图乙中电压的最大值U0需满足U0<
.2d2U1 L2
(3)要保持一个完整波形,需每隔周期T回到初始位置.波形如图3所示.
