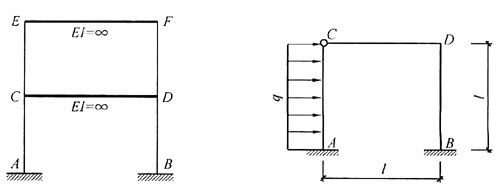
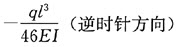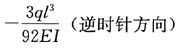(12分)如图甲所示,水平放置的平行金属板A和B的距离为d,它们的右端安放着垂直于金属板的靶MN,现在A、B板上加上如图乙所示的方波形电压,电压的正向值为U0,反向电压值为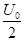 ,且每隔T/2变向1次。现将质量为m的带正电,且电荷量为q的粒子束从AB的中点O以平行于金属板的方向OO′射入,设粒子能全部打在靶上而且所有粒子在A、B间的飞行时间均为T。不计重力的影响,试问:
,且每隔T/2变向1次。现将质量为m的带正电,且电荷量为q的粒子束从AB的中点O以平行于金属板的方向OO′射入,设粒子能全部打在靶上而且所有粒子在A、B间的飞行时间均为T。不计重力的影响,试问:
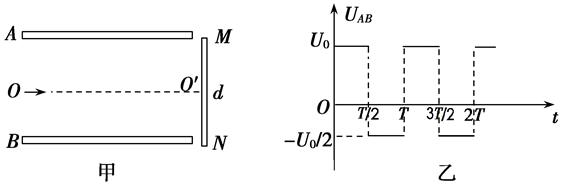
(1)定性分析在t=0时刻从O点进入的粒子,在垂直于金属板的方向上的运动情况。
(2)在距靶MN的中心O′点多远的范围内有粒子击中?
(3)要使粒子能全部打在靶MN上,电压U0的数值应满足什么条件?(写出U0、m、d、q、T的关系式即可)
(1)先向下加速再向下减速。 (2) O′正下方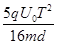 到O′正上方
到O′正上方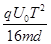 . (3) U0<
. (3) U0<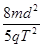 .
.
题目分析:
(1)先向下加速再向下减速。
(2)粒子打在靶MN上的范围,实际上就是粒子在竖直方向所能到达的范围.
当粒子在0,T,2T…nT时刻进入电场中,粒子将打在O′点下方最远处,在前T/2时间内,粒子在竖直方向上的位移
y1=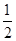 a1
a1 2=
2=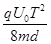
在后T/2时间内,粒子在竖直方向上的位移y2=v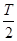 -
-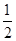 a1(
a1(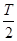 )2
)2
其中v=a1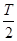 =
= ×
×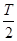 ,a2=
,a2=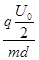
可得y2=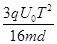
故O′点正下方最大位移y=y1+y2=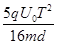
当粒子在T/2,3T/2… T时刻进入电场时,粒子将打在O′点上方最远处,在前T/2时间内,粒子在竖直方向上的位移y1′ =
T时刻进入电场时,粒子将打在O′点上方最远处,在前T/2时间内,粒子在竖直方向上的位移y1′ =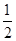 a1′
a1′ 2=
2=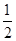
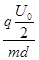
 2=
2=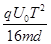
在后T/2时间内,粒子在竖直方向上的位移
y2′=v′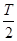 -
-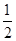 a2′
a2′ 2
2
其中v′=a1′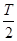 =
=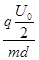 ×
×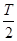 ,a2′=
,a2′=
可得y2′=0
故O′点正上方最大位移y′=y1′+y2′=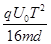 .
.
(3)要使粒子能全部打在靶MN上,则有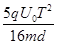 <
<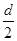 ,即U0<
,即U0<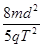 .
.
点评:本题是粒子在周期性变化的电场中运动,分析带电粒子的运动情况是关键.

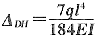 ,方向水平向右,则结点D的角位移
,方向水平向右,则结点D的角位移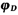 为()。
为()。