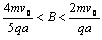问题
计算题
相距2L的AB、CD两平行直线间区域存在着两个方向相反的匀强电场,其中PT上方的电场E1竖直向下;下方的电场E0竖直向上。PQ上连续分布着电量+q、质量m的粒子,依次以相同的初速度v0垂直射入E0中,PQ=L。若从Q点射入的粒子恰从M点水平射出(如图),MT=L/2。不计粒子的重力及相互作用。问:
(1)E0与E1的大小;
(2)若从M点射出的粒子恰从中点S位置垂直射入边长为a的正方形有界匀强磁场区域(如图)。要使粒子能够从最上边界射出磁场区域。则该匀强磁场的磁感应强度B的大小?
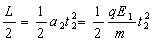
答案
解:(1)设粒子在E0和E1中的时间为t1与t2,到达R时竖直速度为vy,则
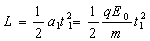
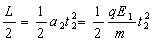
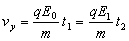
v0(t1+t2)=2L
联立得E1=2E0
即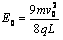 ,
,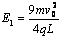
(2)
粒子进入磁场的速度为v0
若粒子恰好从最左上角偏离,则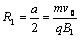
得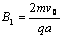
若粒子恰好从最右上角偏离,则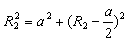
得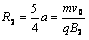 ,即
,即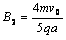
综合得